[DSA] Array

    Data Structure and Algorithm   Data Structure and Algorithm   Array  Comments

What is Array?

可以想像成櫃子，櫃子上有某些連續的編號

–> 有編號的櫃子

Memory is (Generally Viewed as) Array

記憶體就是一個很大的Array

address就是index

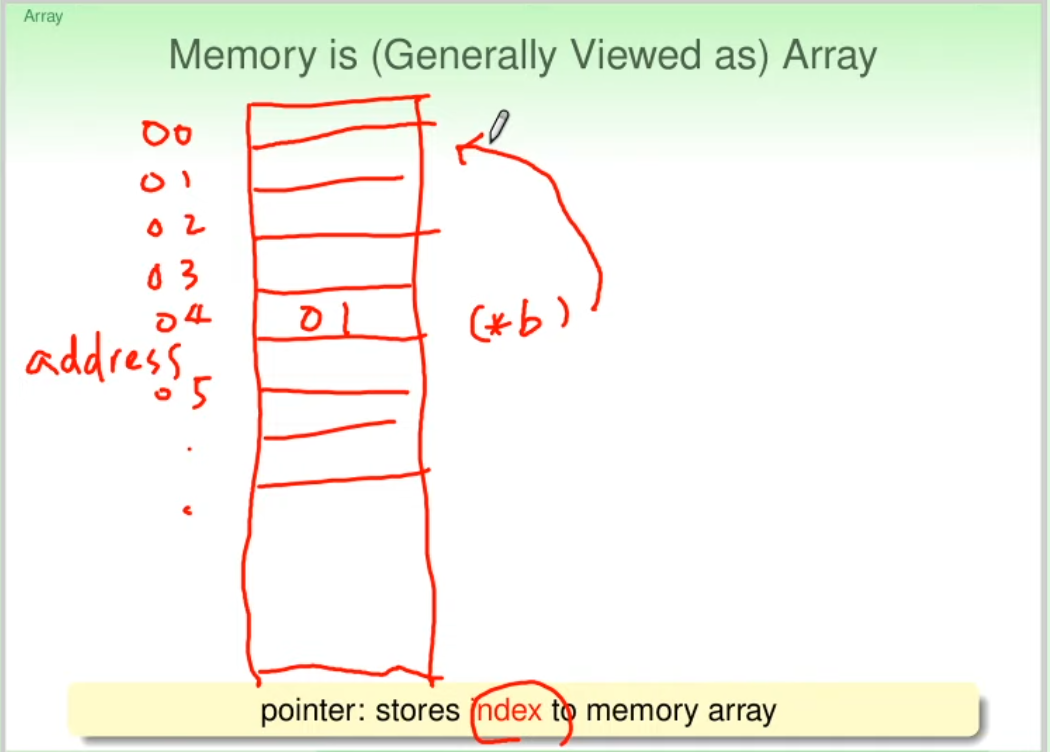
Array as Memory Block in C/C++

反過來說Array也是記憶體

  • Note: 一個 Data Structure 看的是如何取用與維護

Array as Abstract Data Structure

C++ STL Vector: a Growing Array

完整的array implementation

Two Dimensional Array

最熟悉的 Two Dimensional Array: 圖片

One Block Implementation of 2D Array

把2D展開成1D

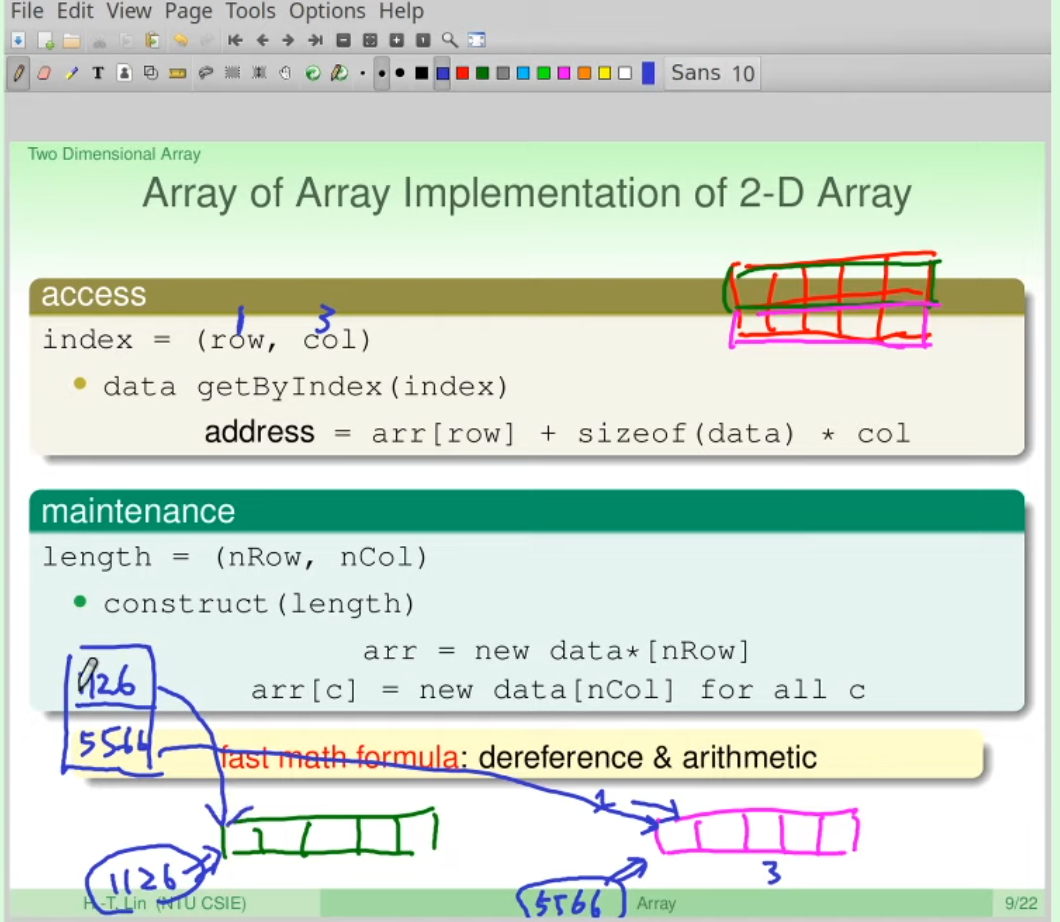
Array of Array Implementation of 2D Array

ex: 第一個raw與第二個raw分開放(每個raw有5個element)

Comparison of Two Implementations

#one blockarray of array
spaceelementselments & nRow pointers
constructfixedprop. nRow
getone dereftwo deref
  • tradeoff:
    • one block: faster & succinct
    • array of array: again easier for programmers

A Table between Two Programs

以下兩種方式，哪種比較快？

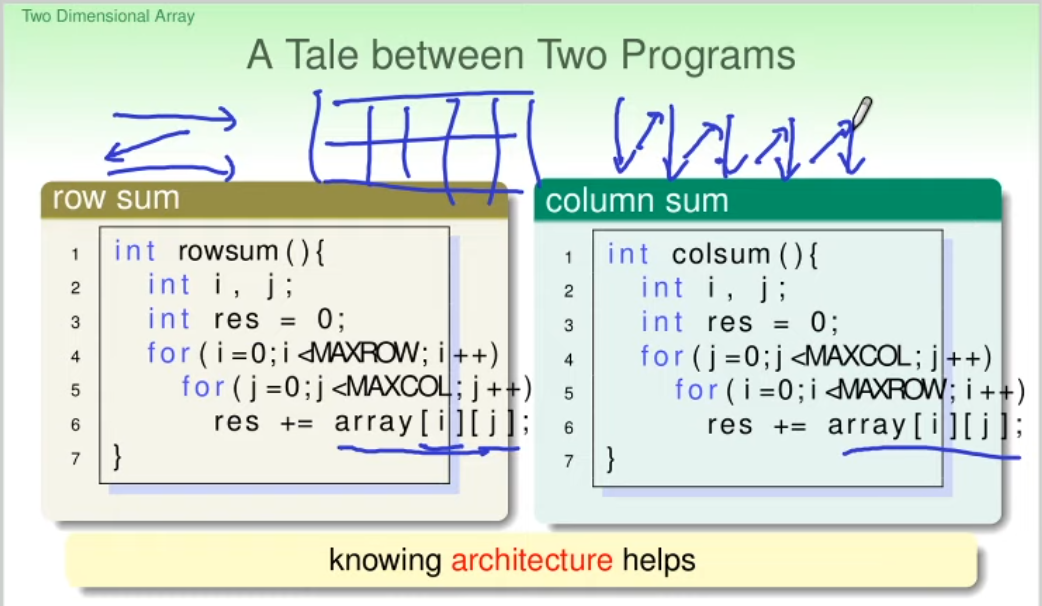
  • Ans: rowsum()

    因為快取機制，rowsum() 是連續的記憶體，比較吃香

Ordered Array

Definition of Ordered Array

An array of consecutive elements with ordered values.

arr[0] <= arr[1] <= arr[2] <= ... <= arr[end-1]

insert of Ordered Array

不能亂插，需考慮值得大小

  • example:

    [2, 6, 7, 13]
         ^
         |
10 -------

Resutl: [2, 6, 7, 10, 13]

  • Maintain Ordered Array

    以前在維護Array時只需要他的開頭(Head)的位置(因為其他位置都可以從開頭算出來)，現在如果要維護Consecutive Array時需要知道array的尾巴(Tail)，這樣才能知道下次要放新東西時該往哪邊繼續放下去(資料的地方到哪)

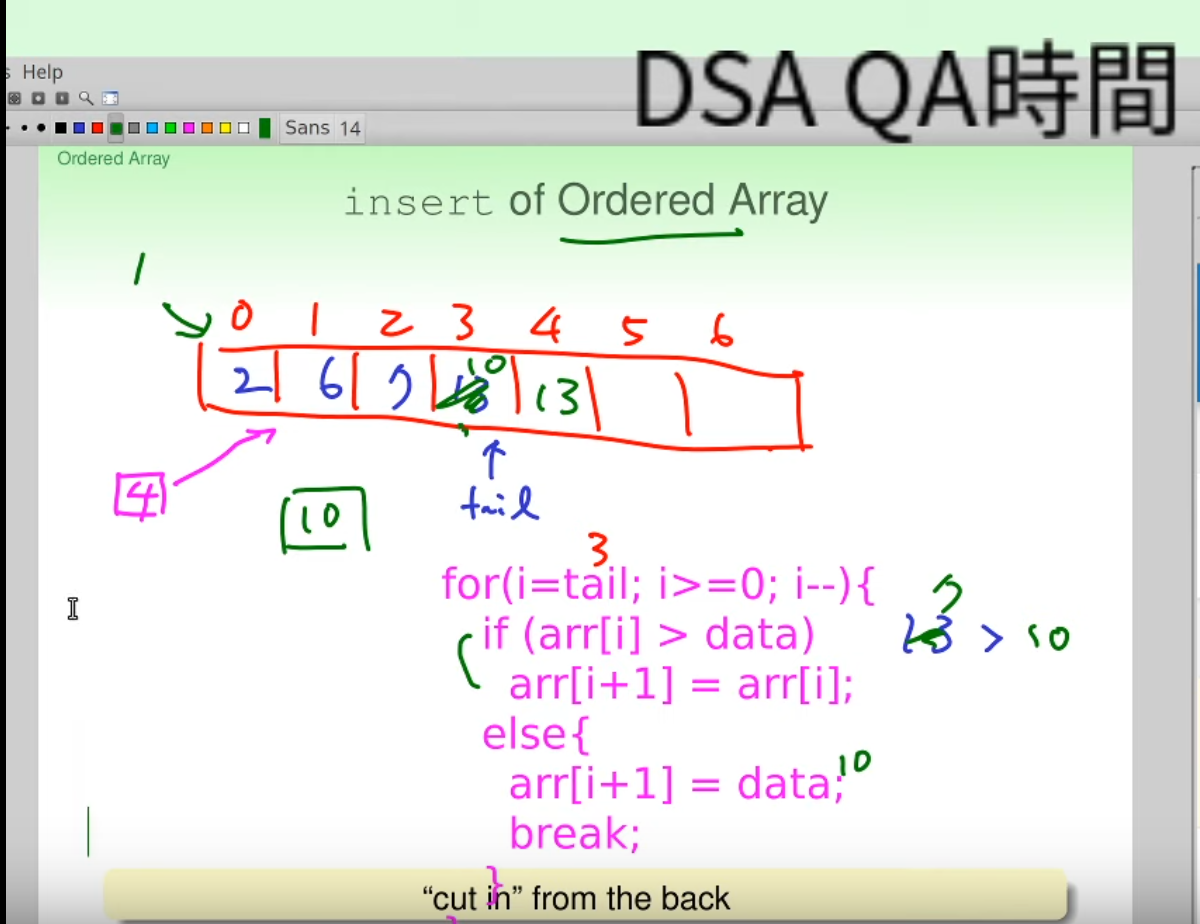
田神: 希望同學有機會想想，修正上面的程式碼～

construct of Ordered Array

Example: 1, 3, 7, 4, 6, 5, 2

Method 1: Selection sort

其中一種方法是使用 getMinIndex()幫我們找出一個Array中最小的，每次叫出最小的，放到new array裡或是與原來的交換，依此類推就可以排出ordered array。 此方法叫做選擇排序法(selection sort)。

getMinIndex multiple times (selection sort)

Method 2: Insertion sort

假設array的左邊是排好序的array(一開始就是index 0)， 右邊是還沒排好的的array(一開始就是index 1~end)，然後從右邊抽一個數字(右邊array的第一個位置)插到左邊，依此類推就可以排出ordered array。

insert multiple times (insertion sort)

update and remove of Ordered Array

Binary Search with Ordered Array

Application: Book Search within (Digital) Library

數位圖書館，每一本書前面有索引(book ID number)，在同一個架子上時書會按照ID大小排序(Ordered Array)

Method 1: Sequential Search Algorithm

已經知道在某個架子上了，那就從左邊找到右邊

for i from 0 to tail
    if (arr[i].ID == toFind.ID)
        return FIND
end for
eturn NOTFIND

此方法並沒有用到ordered array的優點，就算架子上的書沒按照順序排也沒差。

Method 2: Sequential Search Algorithm with Cut (Ordered Array)

Possibly easier to declare not found

toFind.ID = 5566

for i from 0 to tail
    if (arr[i].ID == toFind.ID)
        return FIND
    if (arr[i].ID > toFind.ID)
        return NOTFIND
end for
eturn NOTFIND

Method 3: Binary Search Algorithm (Ordered Array)

begin = 0
end = tail
while (begin != end) {
    mid = (begin + end) / 2

    if (arr[mid] > toFind)
        end = mid - 1
    else if (arr[mid] < toFind)
        begin = mid + 1
    else if arr[mid] = toFind
        FIND
}

Kaka LinSoftware Engineer

AIoT