分類指標 (Classification Metrics)
2024/6/4 updated!
Confuion Matrix (混淆矩陣)
分類器的目的在對樣本進行分類,例如,將樣本中的男女進行區分。不過,在預測分類的過程中,會有預測正確與預測錯誤兩種結果。因此,將分類狀況與預測結果進行排列組合,即可得到以下四種情境:
| Predict Positive | Predict Negative | |
|---|---|---|
| Actual Positive | True Positive (TP) | False Negative (FN) |
| Actual Negative | False Positive (FP) | True Negative (TN) |
Accuracy, Precision, and Recall
Recall 及 Precision 都適合用於
類別不平均的資料集因為在算式中並沒有考慮 True Negatives (TN),只專注於正確判斷正樣本,因此,就算資料集中負樣本的數目遠大於正樣本,Recall 及 Precision 仍是有效的參考指標
Accuracy (準確率)
所有預測為 True 的樣本佔總識別樣本的比例。
- 缺點: 類別比例不均時會影響評價效果
Acc = TP + TN / (TP + TN + FP + FN)
Precision (精確率)
Precision = TP / (TP + FP)
為在所有預測為正樣本中,有多少實際為正樣本。 (針對預測結果)
Recall (召回率; TPR; Sensitive)
就是 True Positive Rate (TPR), 又稱為敏感度 (Sensitive)
Recall = TP / (TP + FN)
表示在所有正樣本中,能夠預測到多少個正樣本。 (針對原來的樣本)
應用場景
1. 當今天你加裝了一個人臉辨識的門鎖時,哪個指標比較重要呢?
Precision(精確率)比較重要,因為你不會希望別人的臉可以打開你家的鎖,判斷成正樣本就一定要是對的
Recall(召回率)低的話就只是常常無法判斷出你的臉,無法開門而已
2. 廣告投放系統
Recall 比較重要,因為重視潛在客戶,我全都要 (實際正向客戶中我預測到多少個)
Precision 就沒那麼重要,不在意預測正向(廣告投出)答對多少
小結
通常在分類問題中,採用 Top N 返回結果的 Precision 和 Recall 來衡量模型的性能,表示為 Precision@N 和 Recall@N。
Precision 高,Recall 低的模型謹慎的模型, 雖然常常無法抓到,但只要有預測到的幾乎都是正確的Recall 高,Precision 低的模型寬鬆的模型, 雖然有可能預測錯誤,但只要是該預測的都可以預測到
Precision 和 Recall 是相反的指標,當分類的 threshold 越高時,Presicion 提高但 Recall 降低,反之則 Precision 降低但 Recall 升高。魚與熊掌不可兼得,如果我們同時想要兼顧兩個指標怎辦呢?這時候就要看 F1-score了。
F1-score (F1-Mesure)
他是
F-score的一個特例,當beta=1時就是F1-score。
F1-score 是 recall 和 precision 的 加權調和平均數,顧名思義就是為了調和 recall 和 precision 之間增減反向的矛盾,對 recall 和 precision 進行加權調和,公式如下:
$$ F1 = 2 * \frac{Precision * Recall}{Precision + Recall}$$
F1-score最理想的數值是趨近於1,就是讓 precision 和 recall 都有很高的值。假設兩者皆為1,則F1-score = 1 (100%),代表該演算法有著最佳的精確度
F-score (F-Mesure)
公式如下:
$$ F = \frac{(1 + \beta^2) * Precision * Recall}{(\beta^2 * Precision) + Recall}$$
beta=0: 就是 Precisionbeta=1: 就是 F1-scorebeta無限大: 就是 Recall
所以當我想多看重一點 Precision 時,beta 就可以選小一點,當我想多看重 Recall 時,beta就可以選大一點。
PR curve and ROC curve
PR curve: 適合類別不均的情況因為是 Precision 與 Recall 並沒有考慮 TN,只專注於正確判斷正樣本,因此,就算資料集中負樣本的數目遠大於正樣本,Recall 及 Precision 仍是有效的參考指標
ROC curve: 適合類別平均的情況
PR Curve (Precision-Recall Curves, 精確召回曲線)
PR 曲線以 Recall 為 X 軸, Precision 為 Y 軸,每一個點代表設定不同的門檻值所得到的不同的 Recall 及 Precision,最後繪製成一條曲線。如下所示:

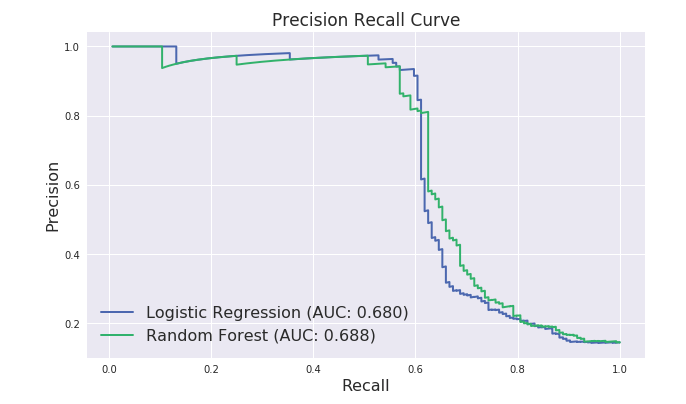
一般來說,Precision 與 Recall 越高,代表模型的效益越高,也就是 PR 曲線越往右上方靠近越好。
ROC Curve (Receiver Operator Characteristic Curve, 接收器工作特性曲線)
ROC 曲線以 FPR (False Positive Rate) 為 X 軸, TPR (True Positive Rate) 為 Y 軸,每一個點代表設定不同的門檻值所得到的不同的 FPR 及 TPR ,最後繪製成一條曲。如下所示:

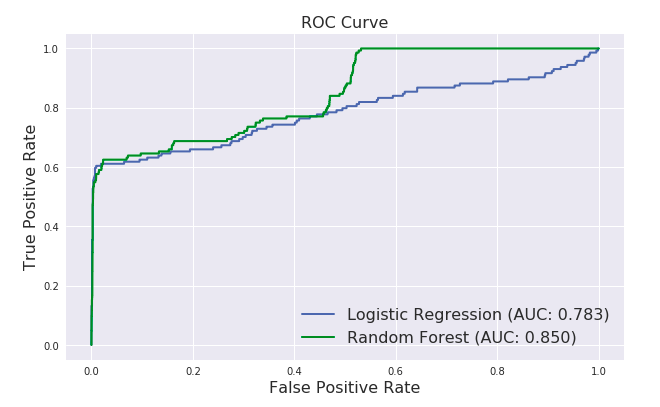
ROC 曲線呈現分類器在效益(真陽性率)與成本(偽陽性率)之間的相對關係。其中點(0,1)代表完美分類,代表效益最大,成本最低。所以ROC 曲線越靠近左上方越好。
FPR (False Positive Rate, 偽陽性率)
FPR 表示成 1-特異度。
特異度(Specificity): 代表正確判斷負樣本的機率。
特異度越高、FPR 越低,模型越能夠正確判斷負樣本、表現越好
公式如下:
Specificity = TN / (TN + FP)
FPR = 1 - Specificity
= FP / (TN + FP)
TPR (True Positive Rate, 真陽性率)
TPR 又稱為敏感度(Sensitivity),它也是我們熟知的召回率(Recall),也就是正確判斷出正樣本的機率。
故 TPR 越高則模型越能夠正確判斷正樣本、表現越好
公式如下:
TPR = Sensitivity = Recall = TP / (TP + FN)
AUC (Area under curve, 曲線下面積)
AUC(Area Under Curve)代表在ROC曲線下的面積,能表示分類器預測能力的一項常用的統計值。前面提到,ROC曲線越靠近左上方越好,因此,ROC曲線下的面積越大越好,代表模型的效益越高。
- AUC = 1: 是完美分類器。絕大多數預測的場合,不存在完美分類器。
- 0.5 < AUC < 1: 優於隨機猜測。這個分類器妥善設定閾值的話,能有預測價值。
- AUC = 0.5: 跟隨機猜測一樣(例:丟銅板),模型沒有預測價值。
- AUC < 0.5: 比隨機猜測還差;但只要進行反預測,就優於隨機猜測。
