Longest Palindromic Substring
- Leetcode: 5. Longest Palindromic Substring
- My solution: kaka-lin/leetcode/00005_longest-palindromic-substring
The detail of explain of solution please see as below.
思路與解法說明請看下面。
Question
Given a string s, return the longest palindromic substring in s
Example 1:
Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.
Example 2:
Input: s = "cbbd"
Output: "bb"
Constraints:
1 <= s.length <= 1000sconsist of only digits and English letters.
Solution
Method 1: Brute-Force (Time Limit Exceeded)
Pick all possible starting and ending positions for a substring, and verify if it is a palindrome.
窮舉所有可能的 Substring,判斷其是否為回文
def longestPalindrome(s):
if not s: return ""
n = len(s)
left, right, longest = 0, 0, 0
for i in range(n):
for j in range(i + 1, n + 1):
substr = s[i:j]
if isPalindrome(substr):
if len(substr) > longest:
left, right, longest = i, j, len(substr)
return s[left:right]
其中判斷是否為回文的方法為:
def isPalindrome(s):
l, r = 0, len(s) - 1
while l < r:
if s[l] != s[r]:
return False
l += 1
r -= 1
return True
- Time-Complexity: $O(n^3)$,
Time Limit Exceeded
Method 2: Dynamic Programming
Python code 直接看這邊。
Step 1. Characterize an OPT Solution
Subproblems:
if s[i~j] is a palindrome, s[i+1~j-1] is also a palindrome.
$$P(i,j) = (P(i+1,j−1)\ and\ S[i] == S[j])$$
Optimal substructure: suppose we already knew that substr
"bab"is a palindrome:Case 1:
"ababa"must be a palindrome因為左右兩端的字母是一樣的
Case 2:
"bbabc"is not a palindrome因為左右兩端的字母不是一樣的
Step 2: Recursively Define the Value of an OPT Solution
Base case:
Odd: $P(i, i) = True$
Even: $P(i, i+1) = (S[i] == S[i+1])$
Example:
odd: abcba i even: a b c c b a i i+1
Recursive case: $P(i,j) = (P(i+1,j−1)\ and\ S[i] == S[j])$
Substring is a palindrome and the two left and right end letters are the same
Step3: Compute Value of an OPT Solution
Bottom-Up Tabulation
建立一個
N x N的表格,如下所示:
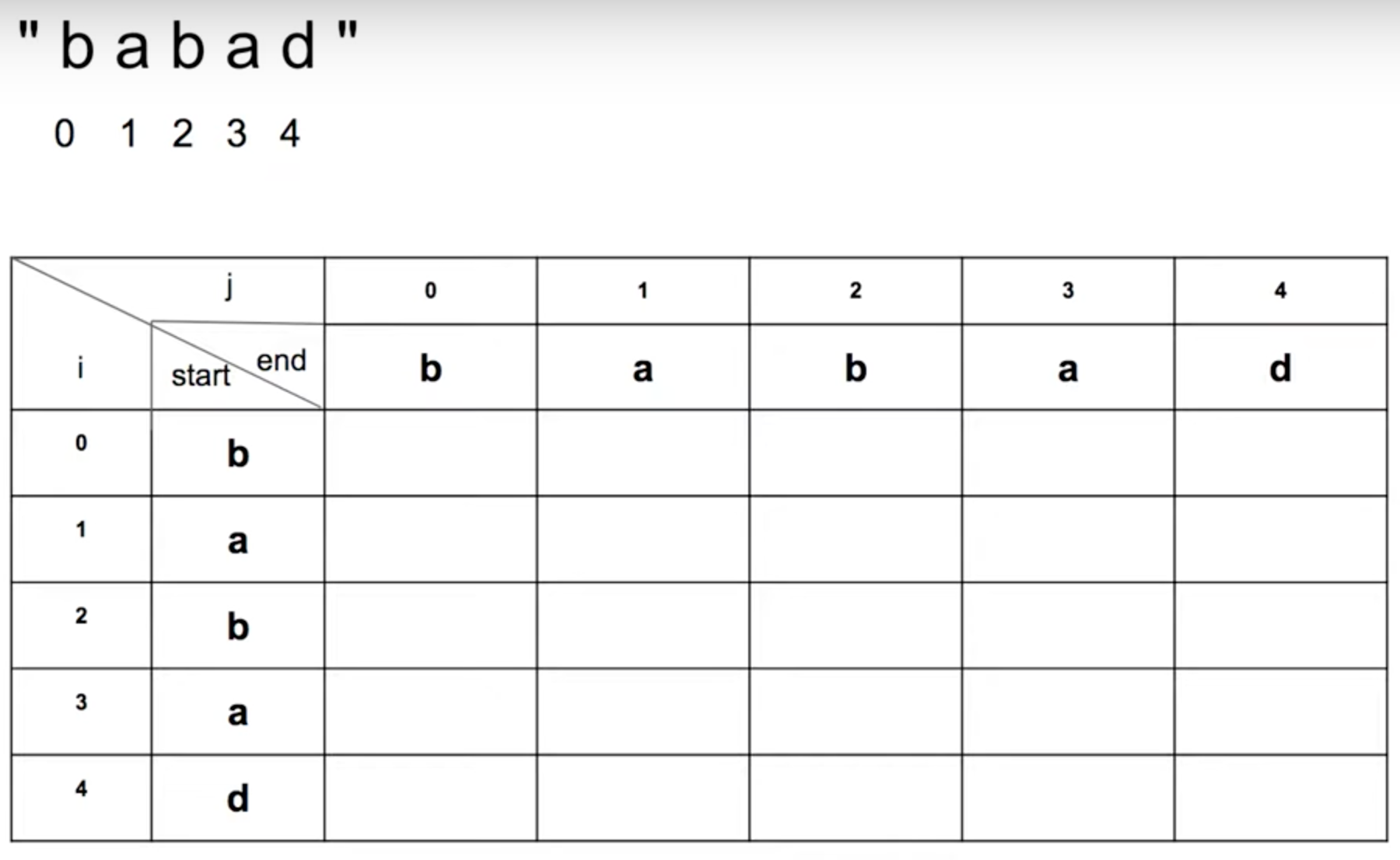
Preporcessing: Base case
在表格中,先填上 Base case 的值 (奇數與偶數情況),如下圖所示:

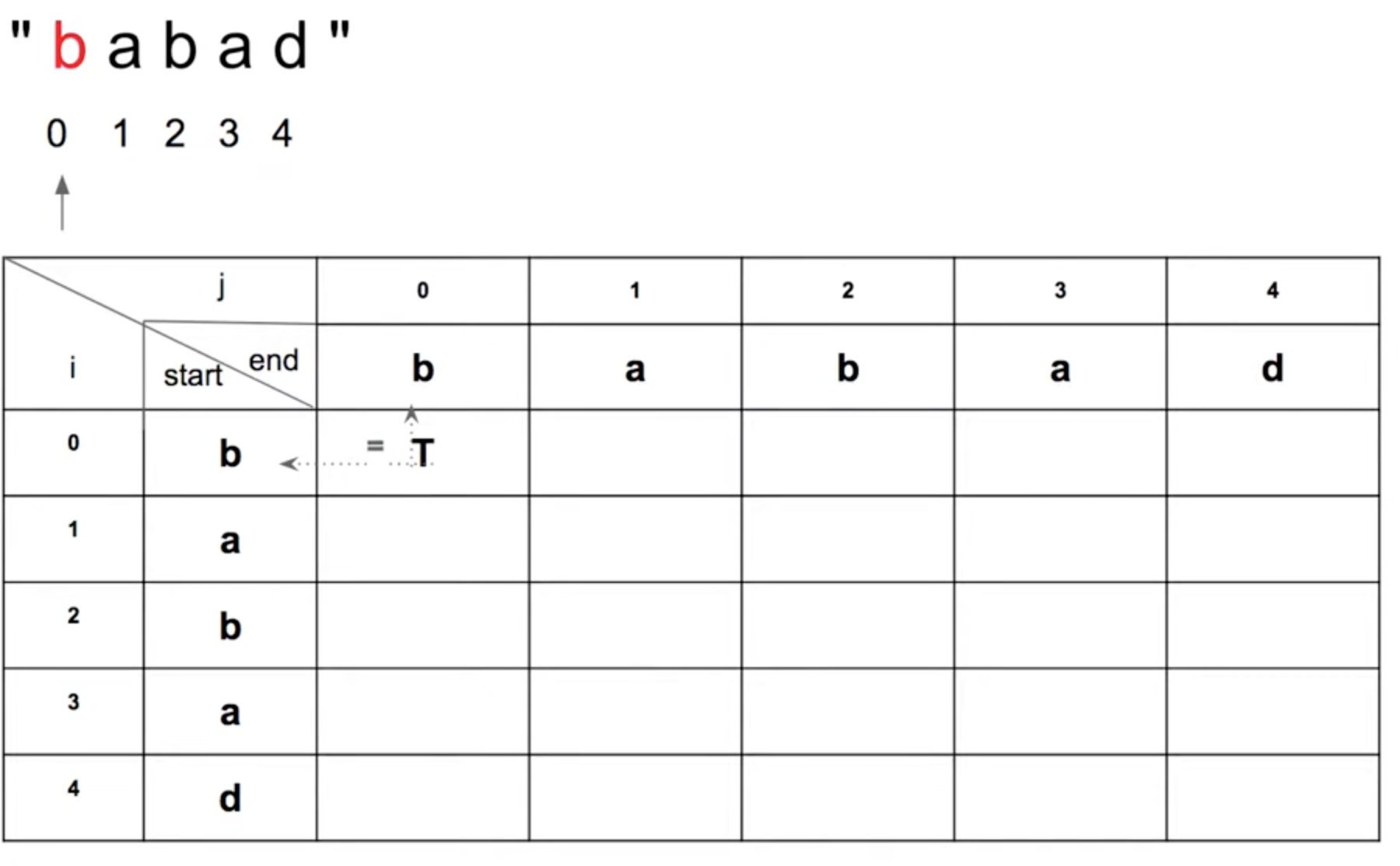
Compute Value
Recursive Case:
$$P(i,j) = (P(i+1,j−1)\ and\ S[i] == S[j])$$
假設 S[i~j] 為回文,那個 S[i+1~j-1] 也必然為回文,依照表格去尋找相對應的值,判斷是否為回文,如下圖所示:

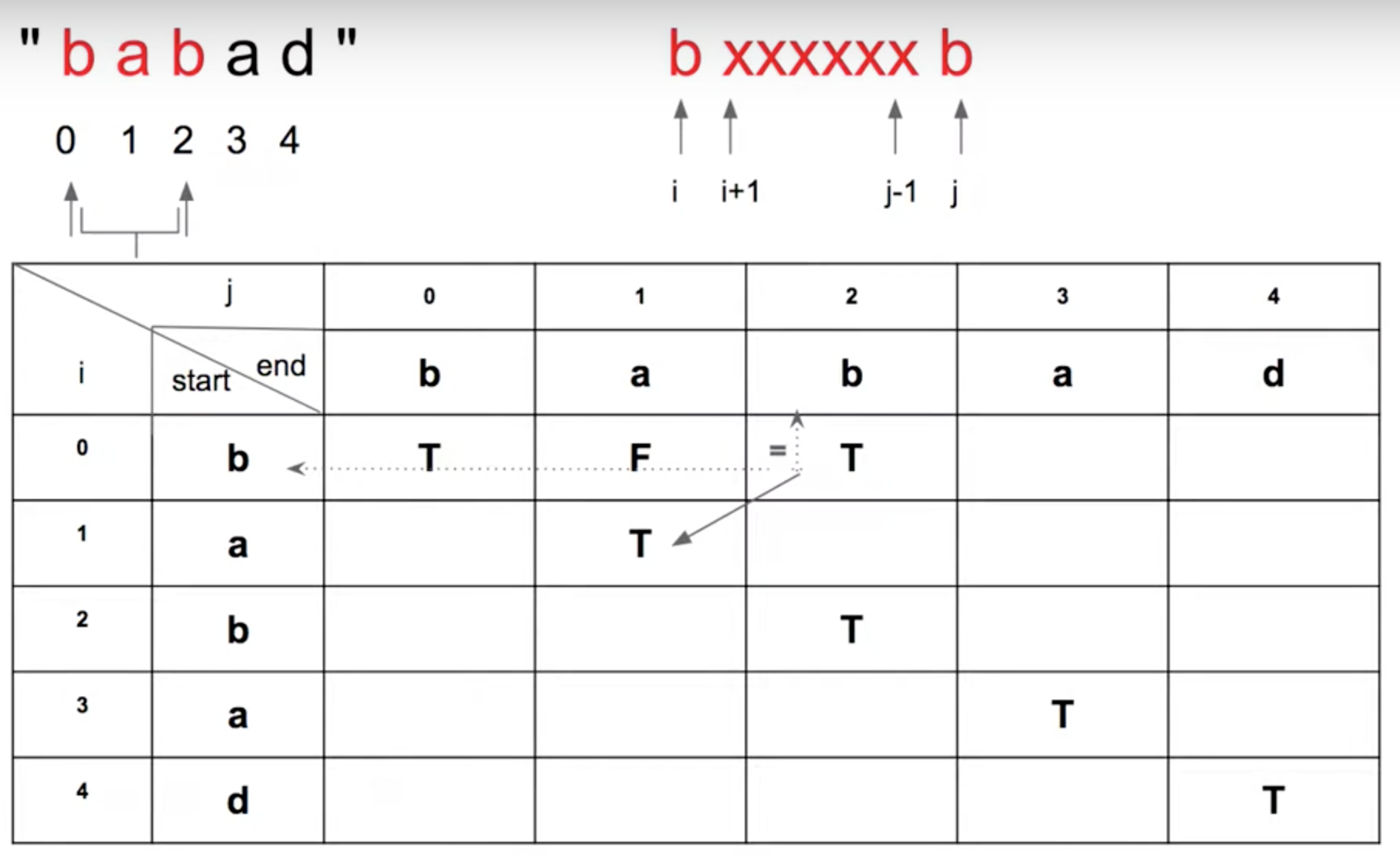
表格 loop 方向
因為 P(i,j) 需要往回查看 P(i+1, j-1),所以我們這邊採用『由上而下由左而右』的方式進行搜索,如下圖所示:

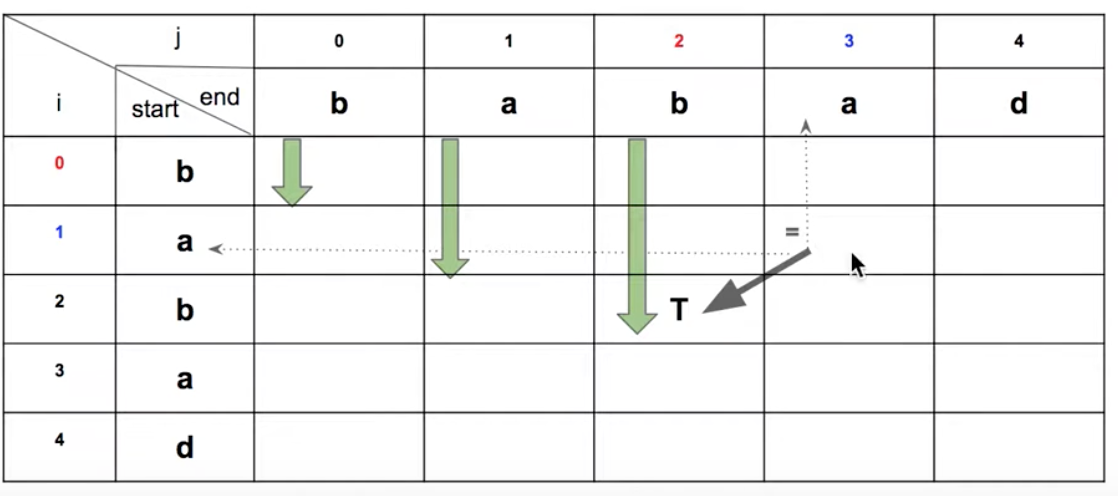
Implementing with Python
# Bottom-Up with Tabulation
def longestPalindrome(s):
n = len(s)
left = right = 0
max_length = 0
p_dp = [[0] * n for _ in range(n)]
# Base case: Odd
for i in range(n):
p_dp[i][i] = True
max_length = 1
left = i
right = i+1
# Base case: Even
for i in range(n-1):
if s[i] == s[i+1]:
p_dp[i][i+1] = True # base case
max_length = 2
left = i
right = i+2
# Recursive case:
# P(i,j) = P(i+1,j−1) and S[i] == S[j]
# 採用『由上而下由左而右』進行搜索。
for j in range(n): # End
for i in range(j-1): # Start
if s[i] == s[j] and p_dp[i+1][j-1]:
p_dp[i][j] = True
if j - i + 1 > max_length:
left = i
right = j+1
max_length = j - i + 1
return s[left:right]
Method 3: Expand Around Center
In fact, we could solve it in O(n^2) time using only constant space.
因為回文特性是繞著中心鏡像出去,所以我們可以從中心擴展(Expand)出去,如下圖所示:

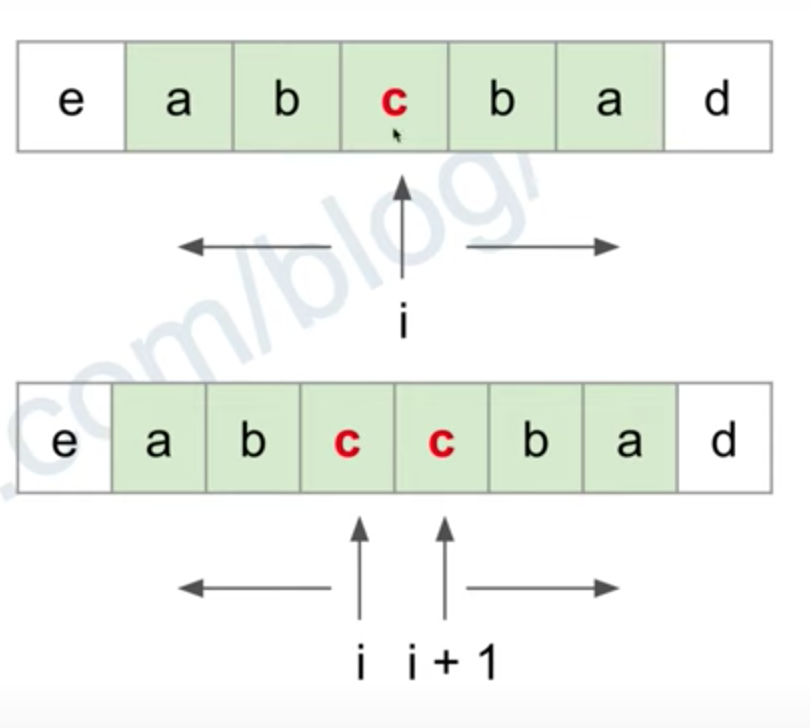
Implementing with Python
從中心擴展:
# get the longest palindrome, l, r are the middle indexes
# from inner to outer
def palindromeAt(s, l, r):
while l >= 0 and r < len(s) and s[l] == s[r]:
l -= 1
r += 1
return s[l+1:r]
分別考慮奇數與偶數的情況,別且都從中心擴展查找最長回文, 並且是比較看誰最長,如下:
def longestPalindrome(s: str) -> str:
ans = ""
for i in range(len(s)):
odd = palindromeAt(s, i, i) # 單數框
even = palindromeAt(s, i, i+1) # 偶數框
ans = max(ans, odd, even, key=len)
return ans
