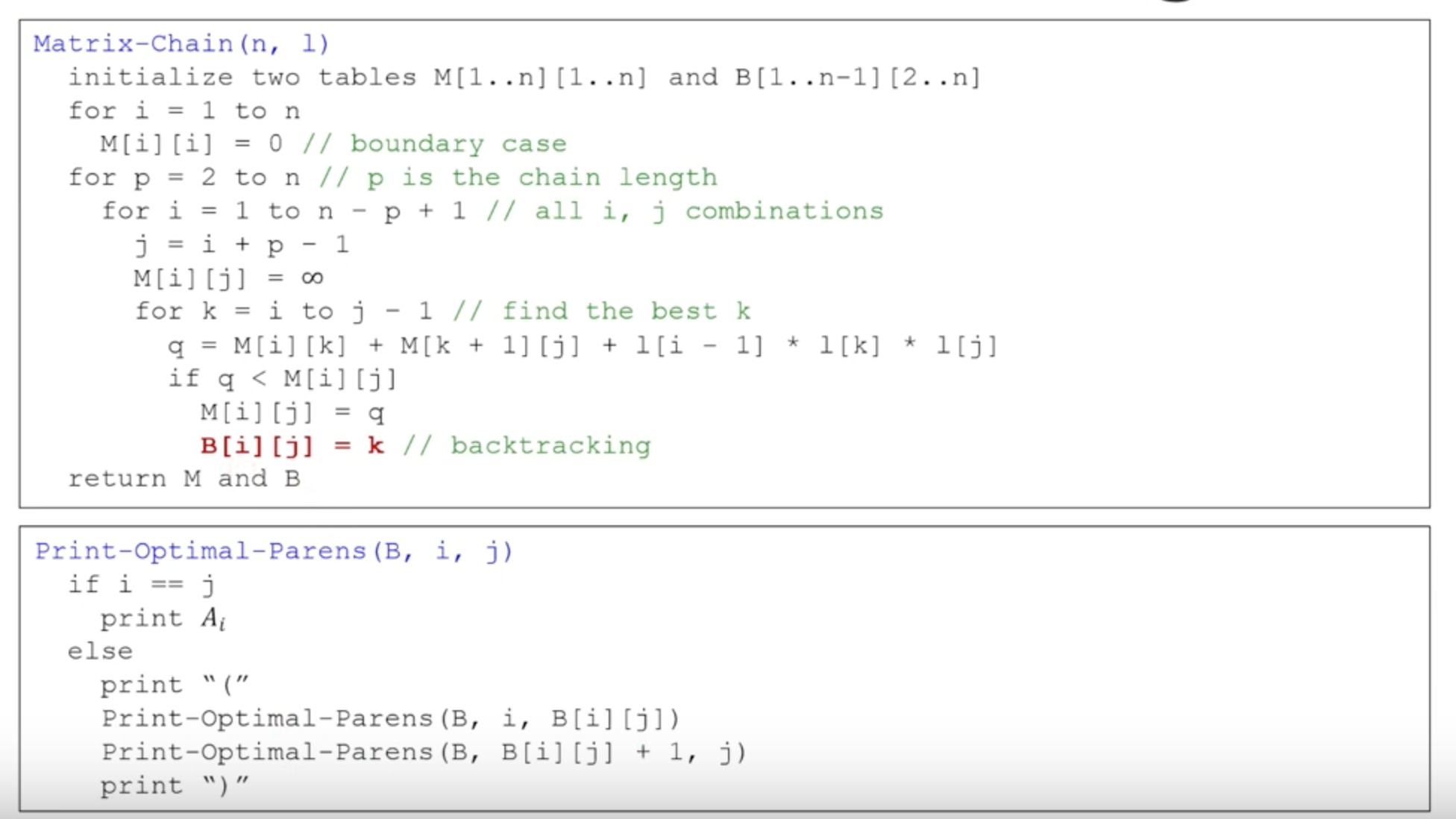
Matrix Chain Multiplication

• Input: a sequence of n matries $(A_1, …, A_n)$

• Output: the product of $A_1A_2 … A_n$

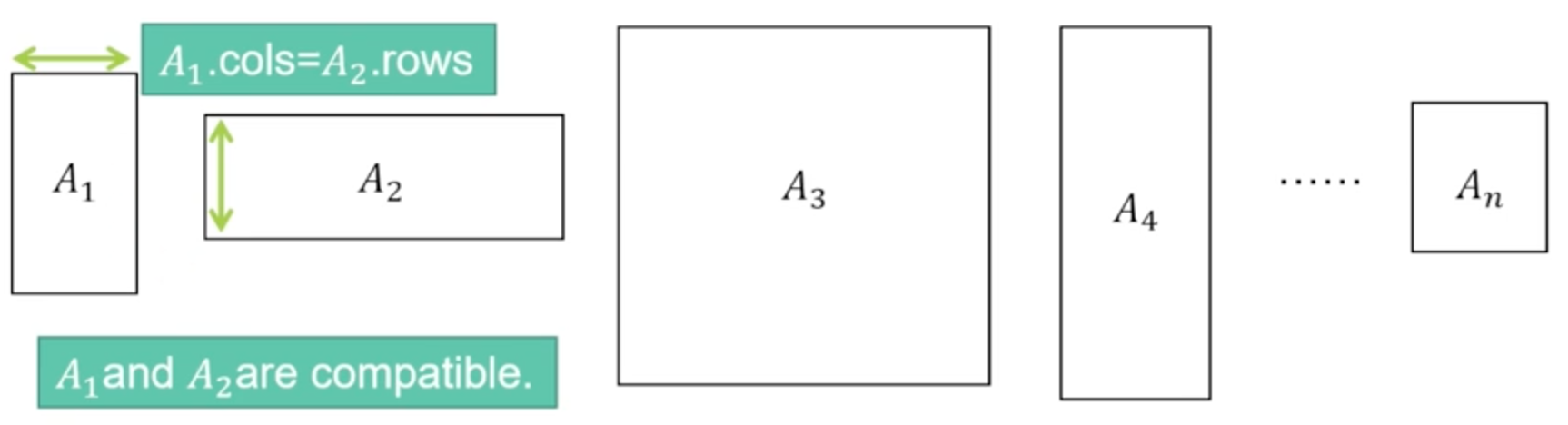
根據 Associative (結合律) 可以將問題重新定義為: Matrix Chain Multiplication Problem

相關說明可參考: Observation

Observation

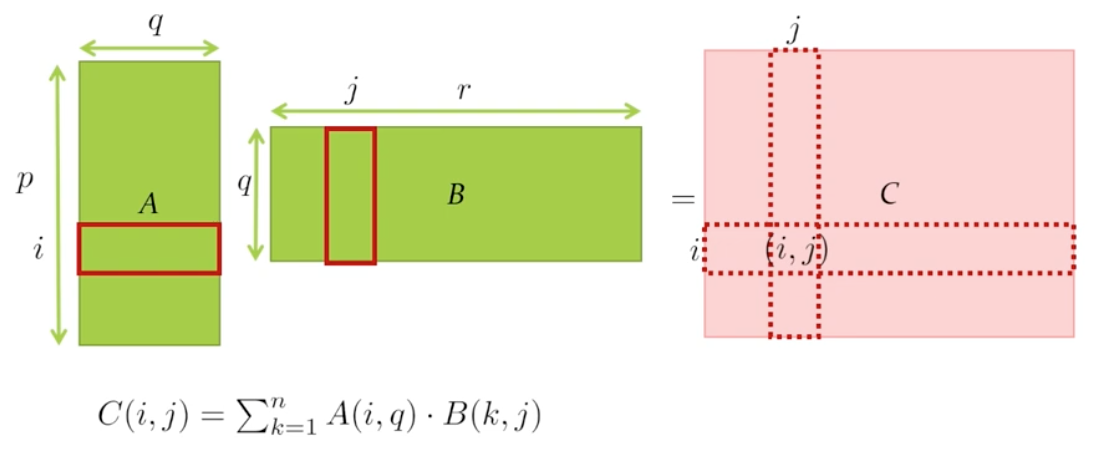
• Each entry takes $q$ multiplications
• There are total $pr$ entries

Time-Complexity: $\Theta(q)\Theta(pr) = \Theta(pqr)$

Associative (結合律)

矩陣相乘是有結合律的，如: A(BC) = (AB)C

在一個包含有二個以上的可結合運算子的表示式，只要運算數的位置沒有改變，其運算的順序就不會對運算出來的值有影響

思考: 能不能找到有效率的乘的方式，減少花的時間

Example:

矩陣相乘為: (nx1) (1xn) (nxn)

如果按照左至右順序相乘，如下圖:

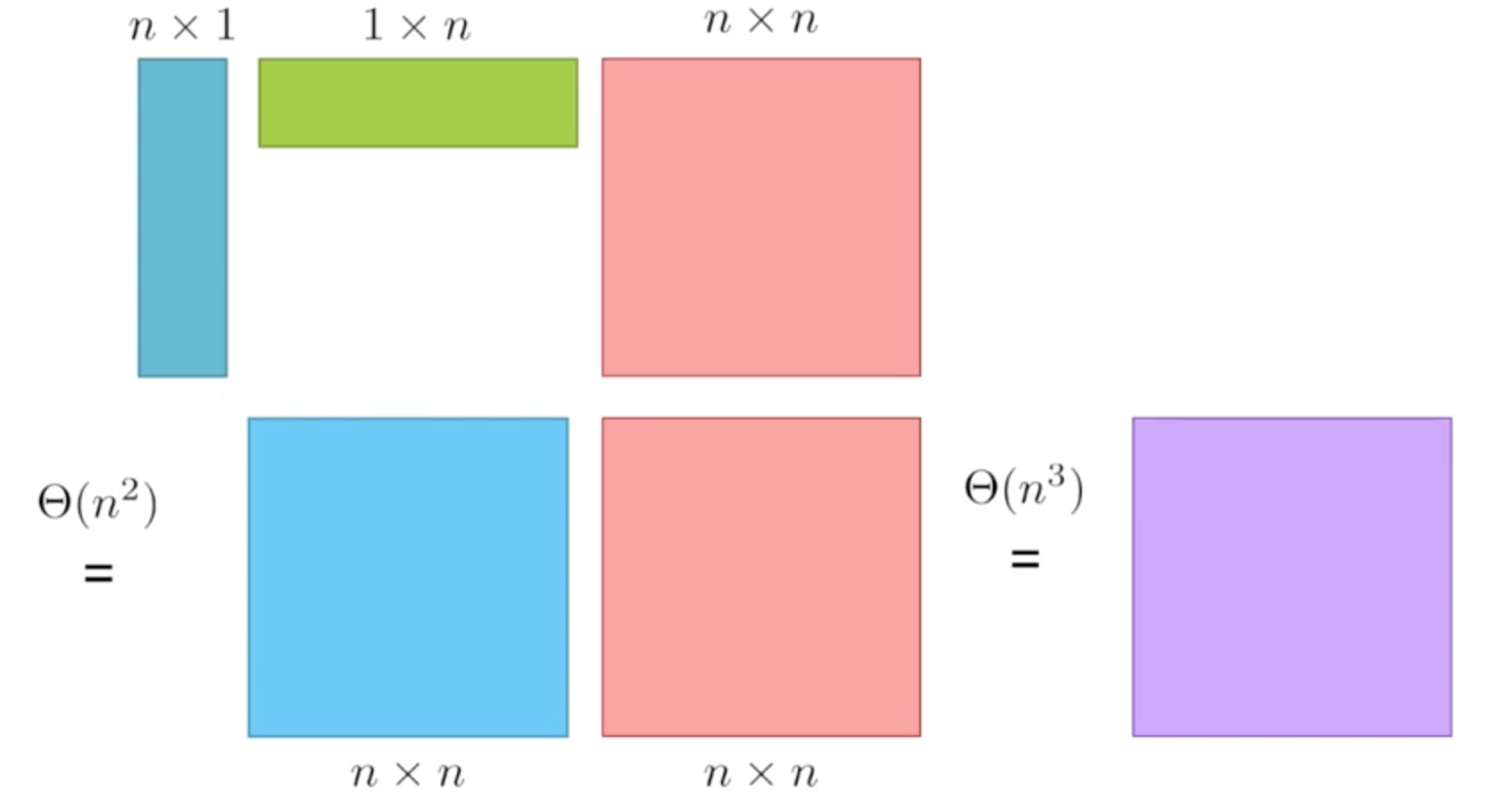
• Overall time is $\theta(n^2) + \theta(n^3) = \theta(n^3)$

但如果我們先將右邊相乘再乘左邊，如下圖:

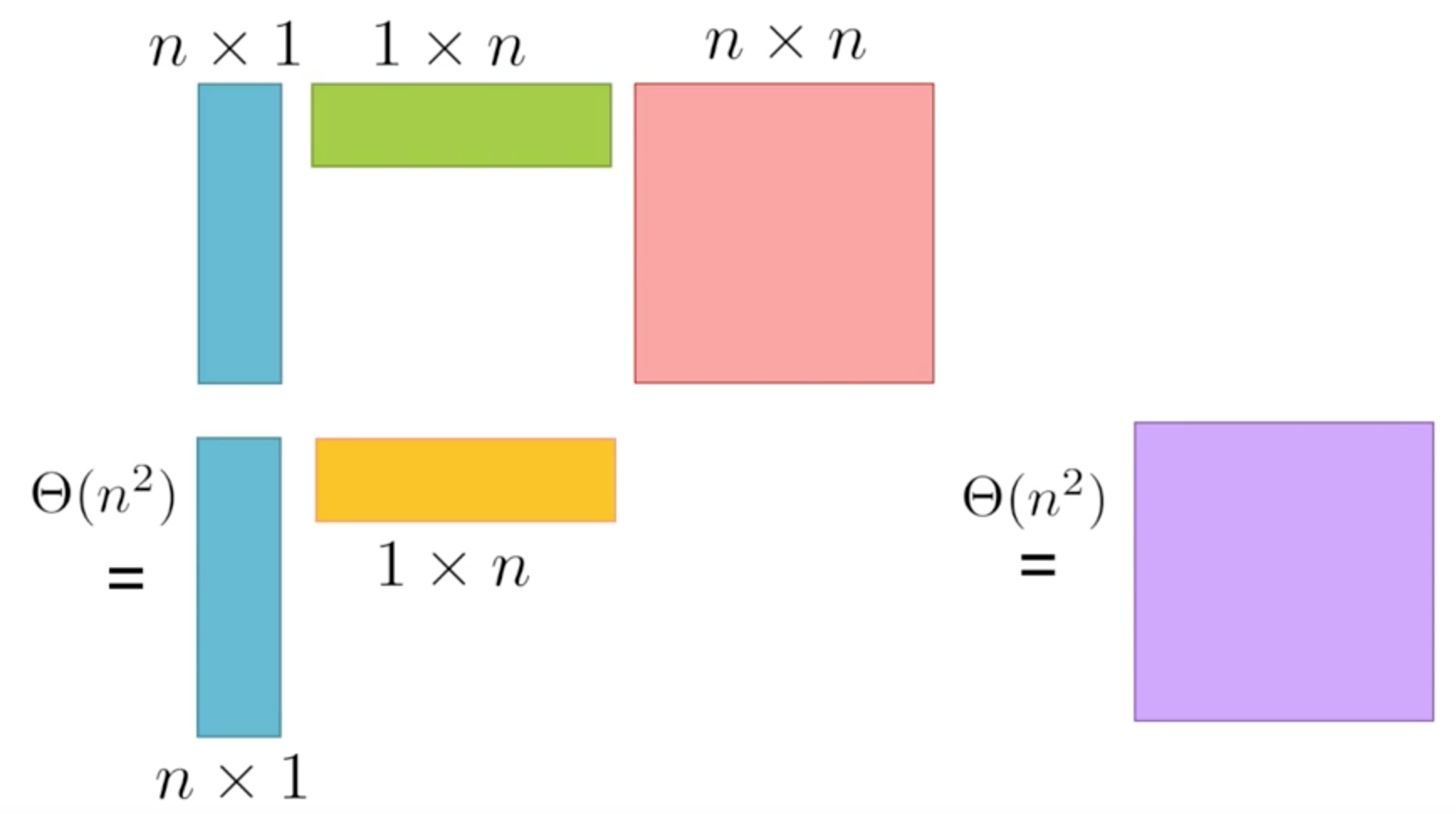
• Overall time is $\theta(n^2) + \theta(n^2) = \theta(n^2)$

> 可以找到一個好的相乘順序，來有效的降低我們的時間複雜度。

Matrix Chain Multiplication Problem

所以我們可以將問題改寫成:

• Input: a sequence of integers $l_0,l_1,…,l_n$

  • $l_{i-1}$ is the number of rows of matrix $A_i$

  • $l_i$ is the number of columns of matrix $A_i$

    Example:

    A1	A2	A3	A4	A5	A6
    30x35	35x15	15x5	5x10	10x20	20x25

    A sequence of integers is: [30, 35, 15, 5, 10, 20, 25]

    For A1: $l_0$ (30) is row, $l_1$ (35) is column

• Output: an order of performing n-1 matrix multiplication in the minimum number of operations to obtain the product of $A_1A_2…A_n$

Brute-Force Algorithm

Dynamic Programming

Step 1. Characterize an OPT Solution

• Subproblems

  • M(i, j): the min #operations for obtain the product of Ai ... Aj

  • Goal: M(1, n)

    長度為 n 的矩陣鏈乘積，表格: M[1~n, 1~n]
    - M[i,j]: Mi..Mj 所需的最小相乘數
    - 目標: M[1,n] (M1M2...Mn的相乘數)
    

• Optimal substructure: suppose we know the OPT to M(i, j), there k cases:

  

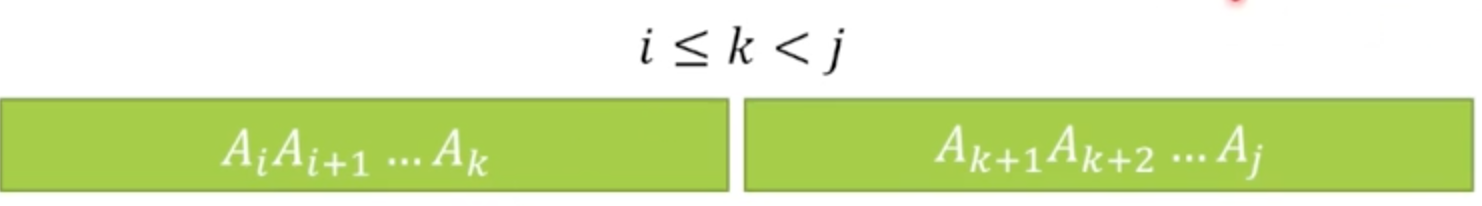
  • Case k: there is cut right after $A_k$ in OPT

    左右花的運算量是 M(i, k), M(k+1, j) 的最佳解
    

  輔助表格 B[1~n, 1~n]: 記錄分割位置 k
  - B[i,j]紀錄哪一個分割位置 k 造就了 M[i,j]的最小純量相乘數
  

Step 2: Recursively Define the Value of an OPT Solution

• Suppose we know the OPT to M(i, j), there k cases:

  • Case k: there is cut right after $A_k$ in OPT

    $$M_{i,j} = M_{i,k} + M_{k+1,j} + l_{i-1}l_jl_k$$

    where:

    • $M_{i,k}$: 左半邊的 optimal solution 所花的相乘時間

    • $M_{k+1,j}$: 右半邊的 optimal solution 所花的相乘時間

    • $l_{i-1}l_jl_k$: 左右半邊乘起來所花的時間。$A_{i…k}A_{k+1…j}$

      

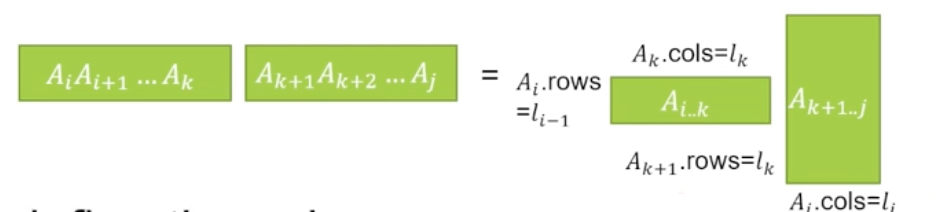
• Recursively define the value:

  

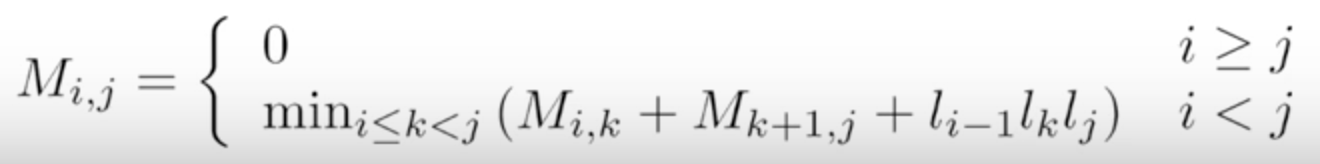
Step3: Compute Value of an OPT Solution

Bottom-Up method

How many subproblems to solve:

• $combination of the values i and j s.t. $1\leq i\leq j\leq n$

  $$T(n) = C_{2}^n + n = \Theta(n^2)$$

  • $C_{2}^n$: $i\neq j$
  • $n$: $i = j$

• $T(n) = \Theta(n^3)$

Implement with Python

Input:

A sequence of integers l is: [30, 35, 15, 5, 10, 20, 25]

所以維度 list 的長度 = 所須相乘矩陣數量 + 1

Recursive case:

$$M_{i,j} = M_{i,k} + M_{k+1,j} + l_{i-1}l_jl_k$$

Table M:

*** p 就是從對角線開始往右上遍歷 (每一個橫排)，如下:

n = 5
for p = 2 to n
  for i = 1 to n - p + 1
    j = i + p - 1

      1 2 3 4 5
1     x # $ % @ | p = 5 (@)
2     0 x # $ % | p = 4 (%)
3     0 0 x # $ | p = 3 ($)
4     0 0 0 x # | p = 2 (#)
5     0 0 0 0 x | p = 1 (x)

• 表格詳細說明請看: 如何建立及填表格

Python Code:

def matrix_chain_product(l, n):
    """
    Matrix Chain Multiplication:

    given a list of integers corresponding to the dimensions
    of each pair of matrices forming a chain.

    Args:
        l: A list of integers corresponding to the dimensions.
        n: The length of l

    Returns:
        M: is the minimum number of scalar multiplications needed
          to compute the product of matrices A(i), A(i+1), ..., A(j)
        B: is the index of the matrix after which the product
          is split in an optimal parenthesization of the matrix product.
    """
    # Initialize: Build the table
    M = [[0] * n for _ in range(n)]
    B = [[0] * n for _ in range(n)]

    # Base case: 1~n 對角線上皆為 0
    for i in range(1, n):
        M[i][i] = 0

    # compute table
    for p in range(2, n): # p is the chain length (subsequence lengths)
        for i in range(1, n - p + 1): # all i, j combinations
            j = i + p - 1
            M[i][j] = sys.maxsize
            for k in range(i, j): # find the best k
                q = M[i][k] + M[k + 1][j] + l[i-1]*l[k]*l[j]
                if q < M[i][j]:
                    M[i][j] = q
                    B[i][j] = k
    return (M,B)

[補充說明]: 如何建立及填表格

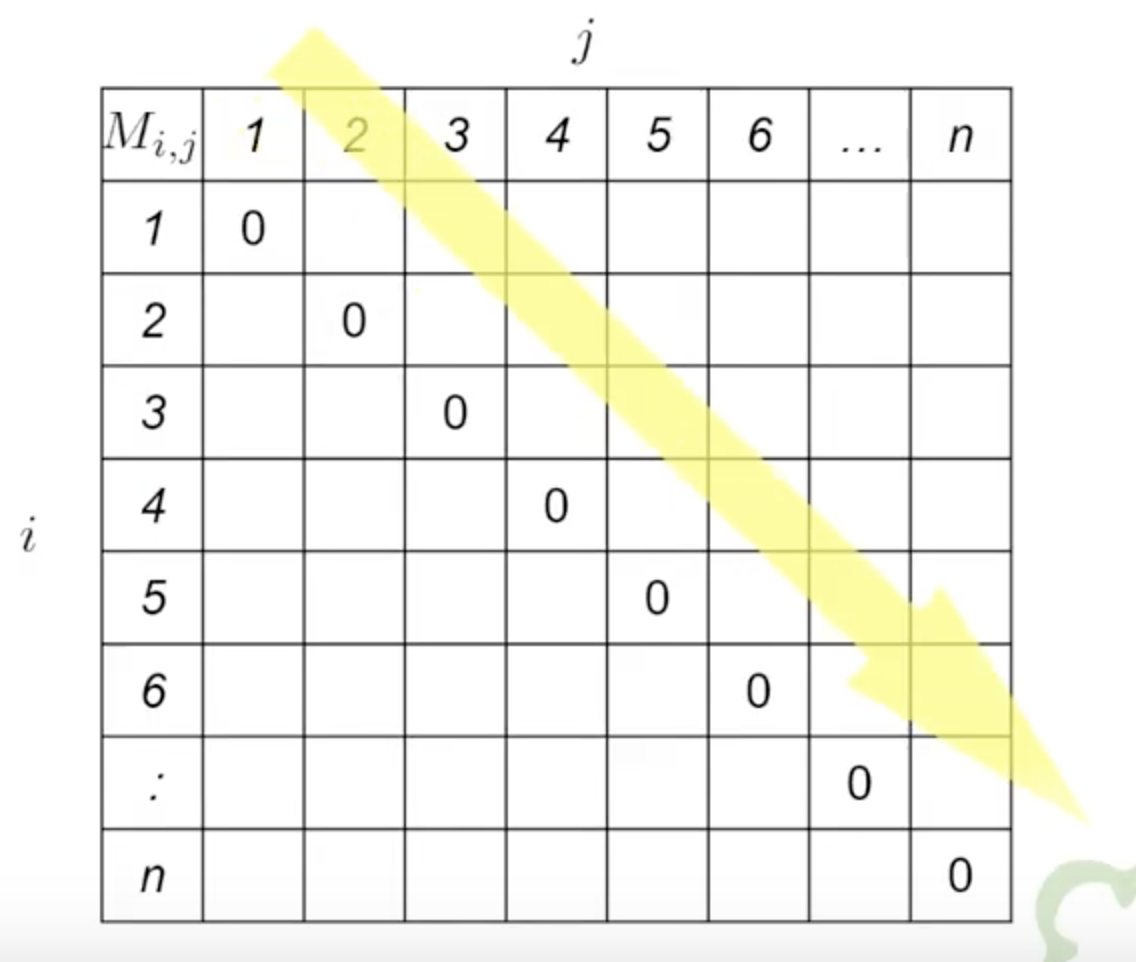
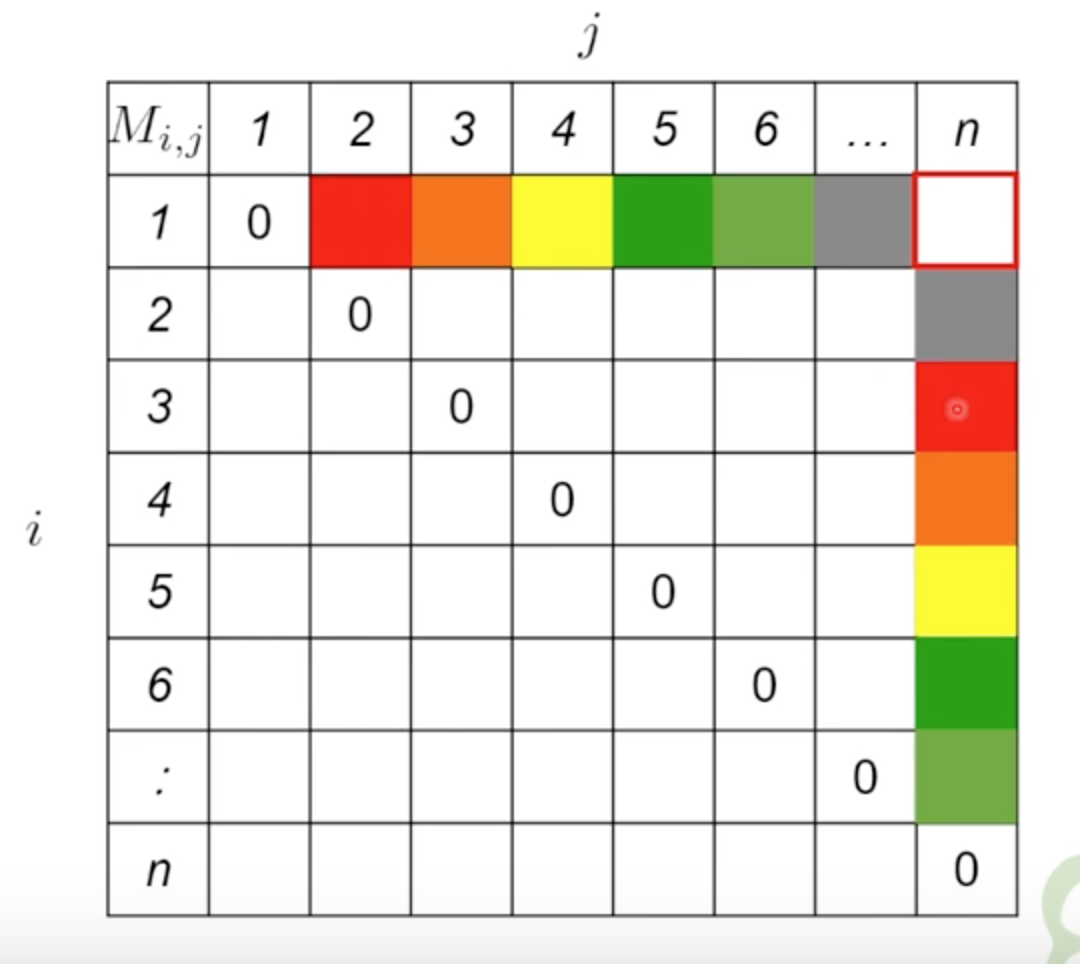
以紅色舉例說明:

M(1, 2), M(3, n)
-> 代表切在 A2，所以 A1A2 要先處理，A3..An要先處理
-> 然後再將兩個相乘

Example:

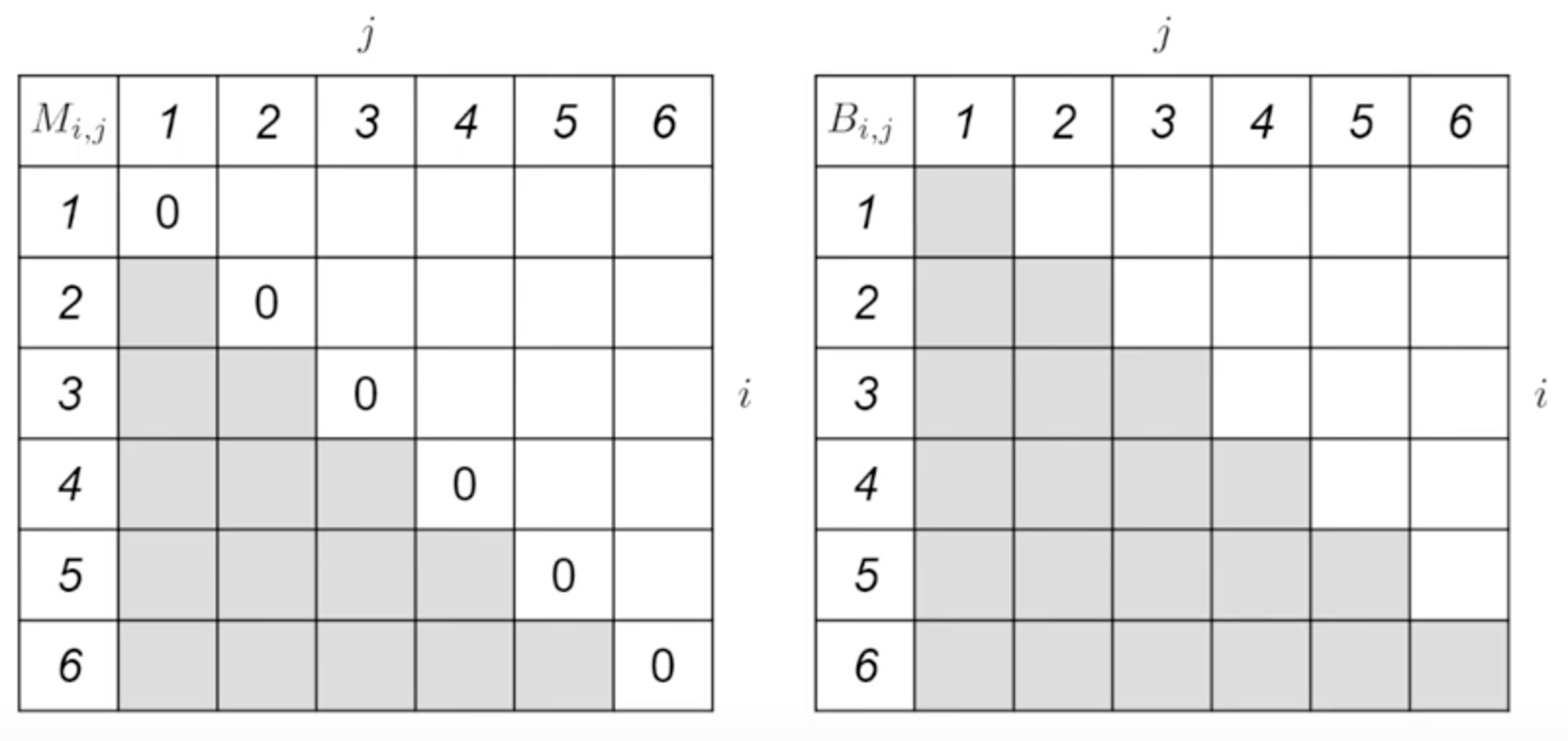
首先第一條斜線就是左右相乘，如:

A1 x A2 = (30x35) x (35x15)
=> T(pqr) = 30 x 35 x 15 = 15750

依此類推，如下圖所示:

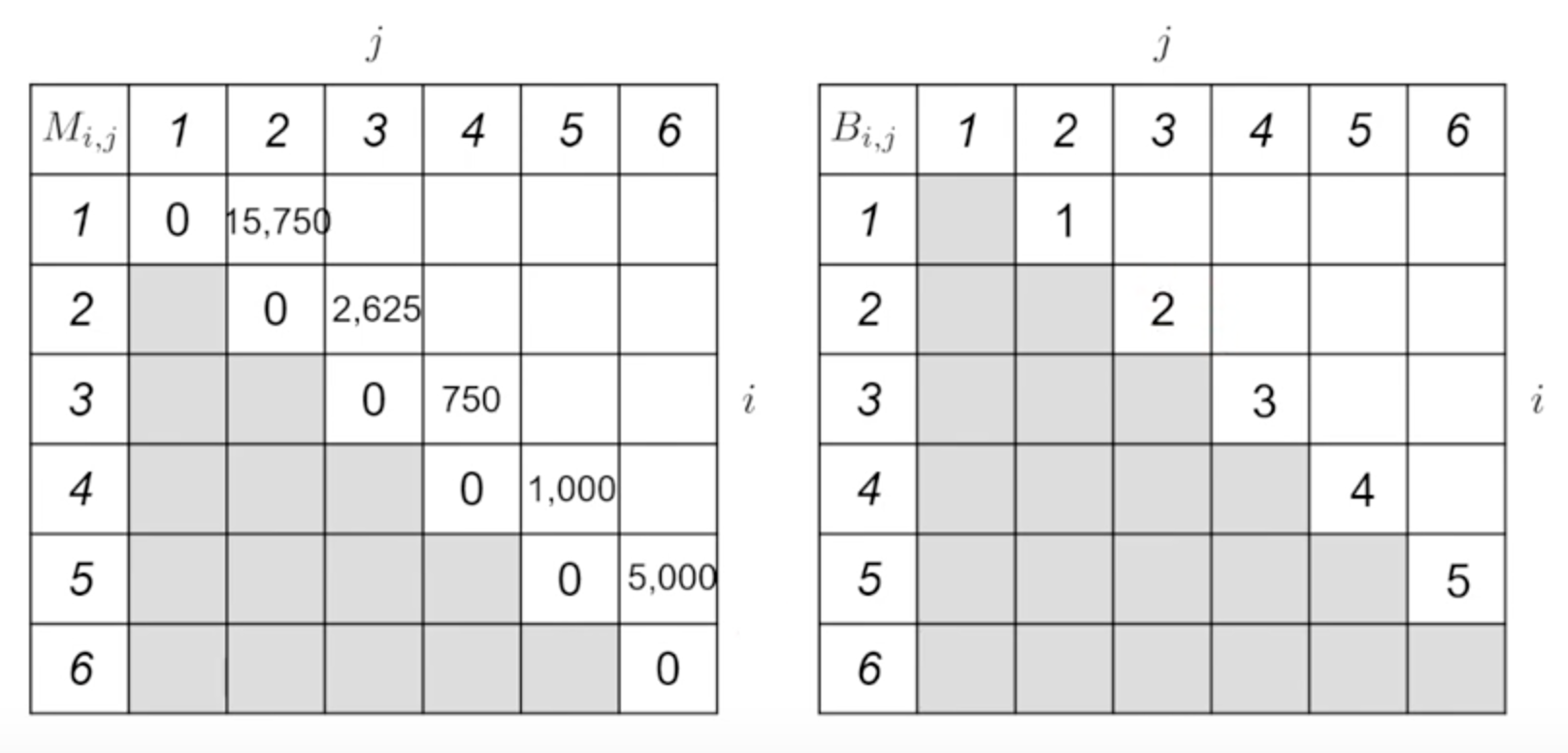
第二條斜線則是要根據左邊與下面的表格來判斷，如:

$M_{1,3}$ 有兩種方式:

1. $M_{1,2}$ + $M_{1,2} * A_3$ 的時間 (從左邊)

M(1,2) x A3 = (30x15) x (15x5)
=> T(pqr) = 30 x 15 x 5 = 2250

M(1,2) + M(1,2) x A3 = 15750 + 2250
                     = 18000

2. A1 * $M_{2,3} + $M_{2,3}$ 的時間 (從下面)

A1 x M(2,3) = (30x35) x (35X5)
=> T(pqr) = 30 x 35 x 5 = 5250

A1 x M(2,3) + M(2,3) = 5250 +2625
                     = 7875

可得 $M_{1,3}$:

• 切點為 1 (A1): B(1,3) = 1

• 計算花費時間為 7875: M(1, 3) = 7875

  先乘 A2, A3 最後再乘 A1 (切點為A1)
  

如下所示:

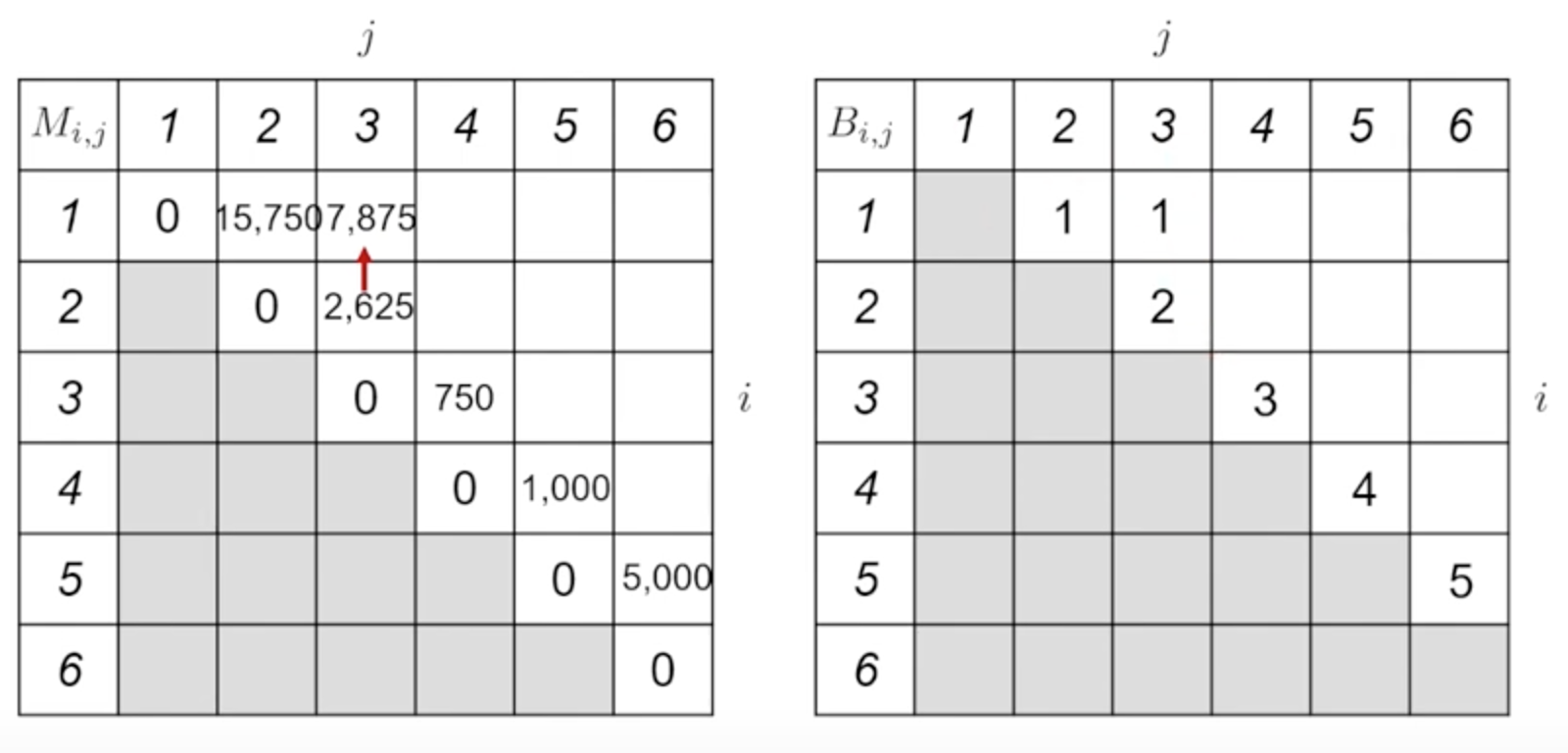
依此方法依序完成表格，如下所示:

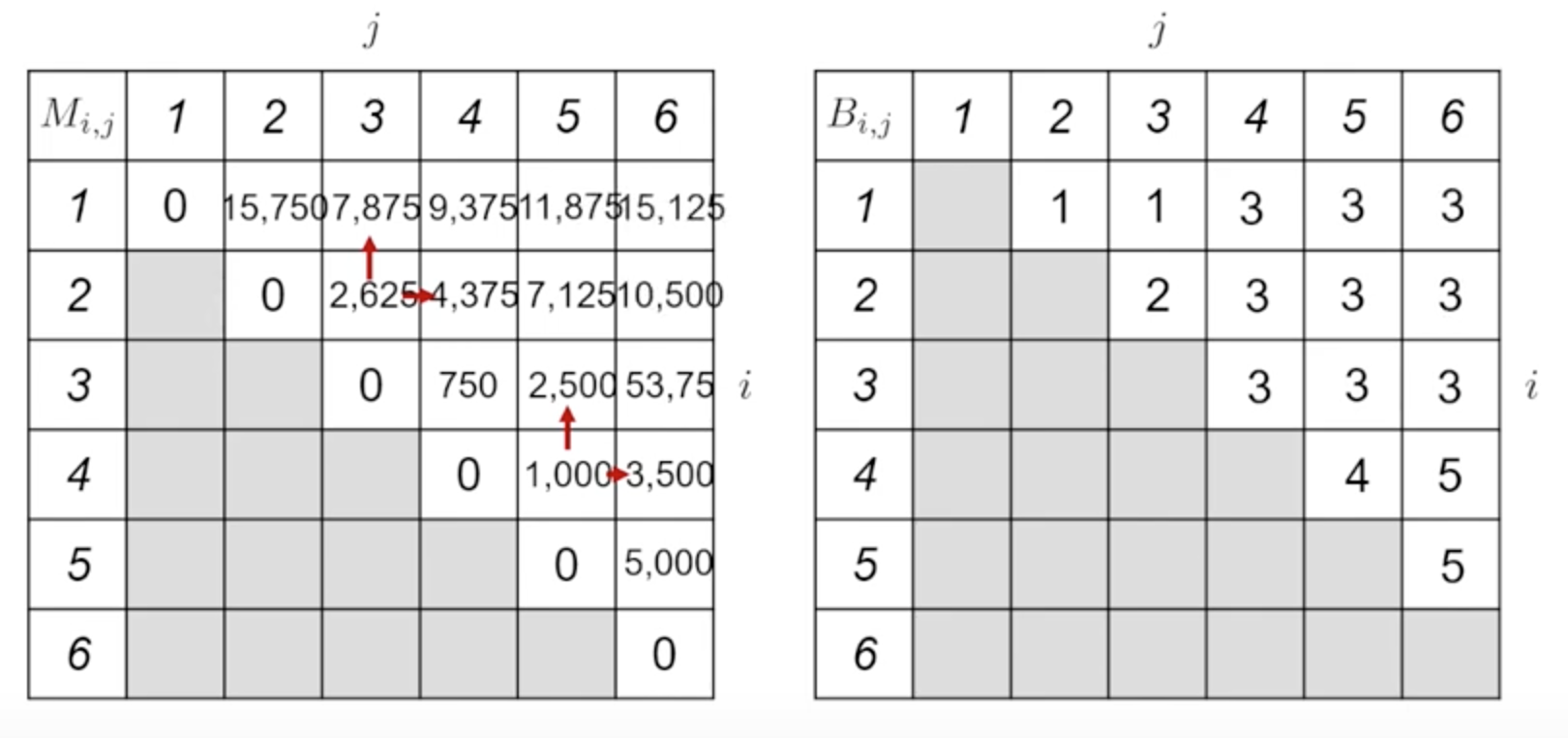
所以最後根據表格可得:

M(1,6) = M(1,3) x M(4,6)
       = (A1(A2A3)) x ((A4A5)A6)

如下圖所示:

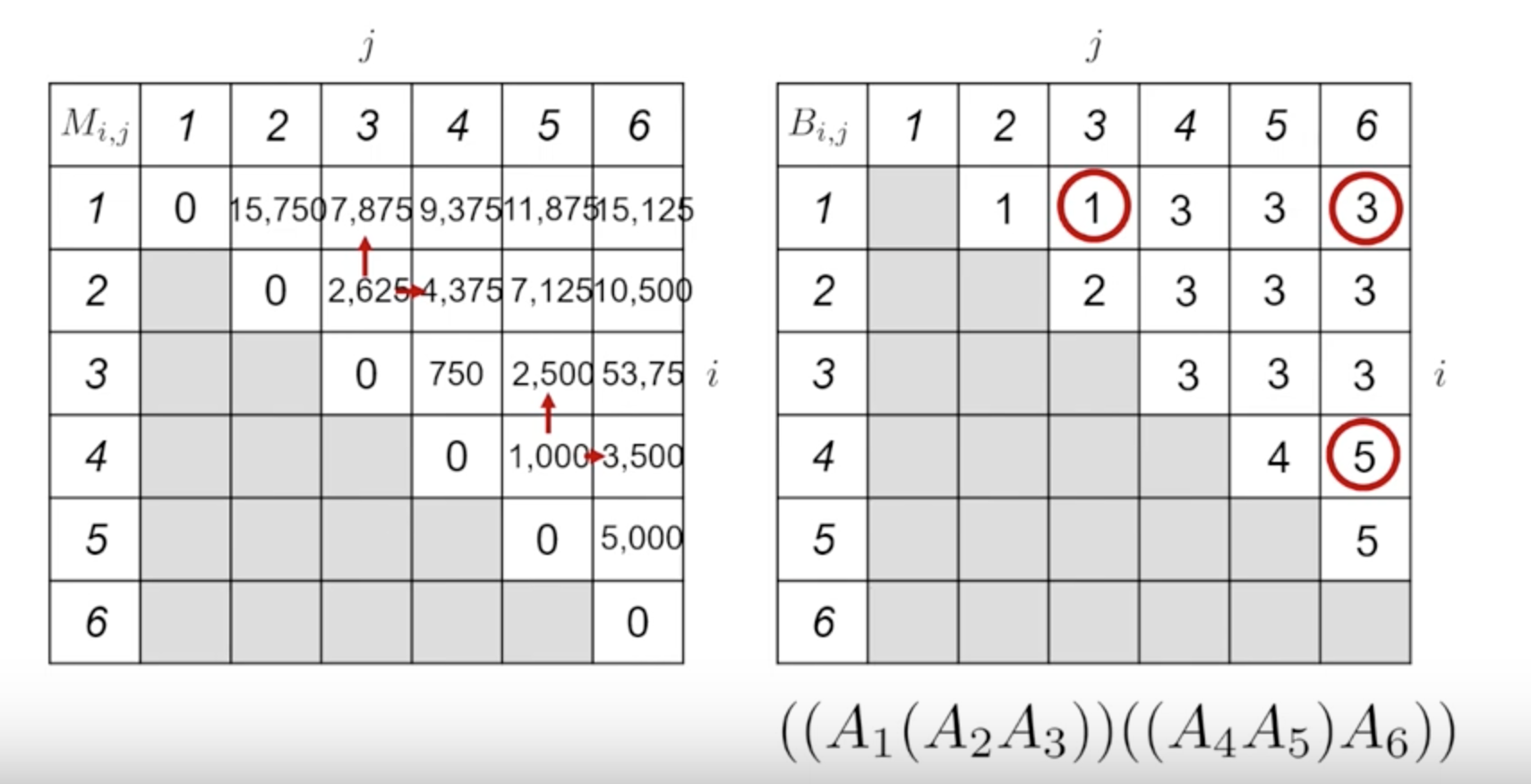
Step4: Construct an OPT Solution by Backtracking

Reference

• 台大資訊 演算法 | ADA 5.4: Matrix-Chain Multiplication