[DSA] 2-3-4 Tree 介紹

    Data Structure and Algorithm   Data Structure and Algorithm   Tree  Comments

2-3-4 Tree

是一種 self-balancing tree (Balanced Tree)。 比紅黑樹容易了解，但不容易 implement，所以不實用。

與 AVL Tree 相比: 用暫存維持平衡性，不會 rebalance immediately

所謂的 2-3-4 tree 就是每個節點可以有2, 3 或 4個子節點。如下:

  • 滿足二元搜索樹的基本性質 - 左小右大，但不是二元樹 (因為可以有很多個子節點)。

  • 節點可以放 1, 2 或 3 個元素 (有 2, 3, 或 4 個 children)如下:

    • 2-節點: 它包含 1 個元素和 2 個子節點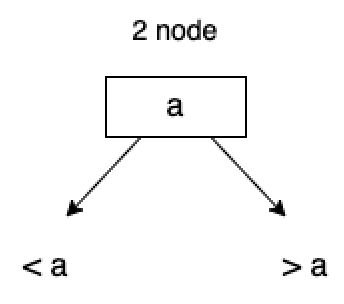

    • 3-節點: 它包含 2 個元素和 3 個子節點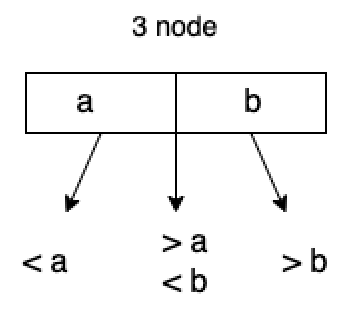

    • 4-節點: 它包含 3 個元素和 4 個子節點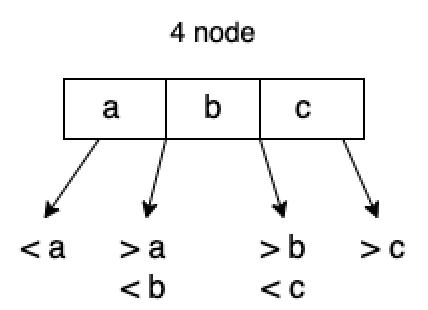

  • 是一棵絕對平衡的樹: h = O(log n)

    左右子樹高度一定相同，所有葉節點(leaf)皆在同一level

    嚴格定義: null 節點皆在同一個 level。(蟑螂腳都要一樣高)

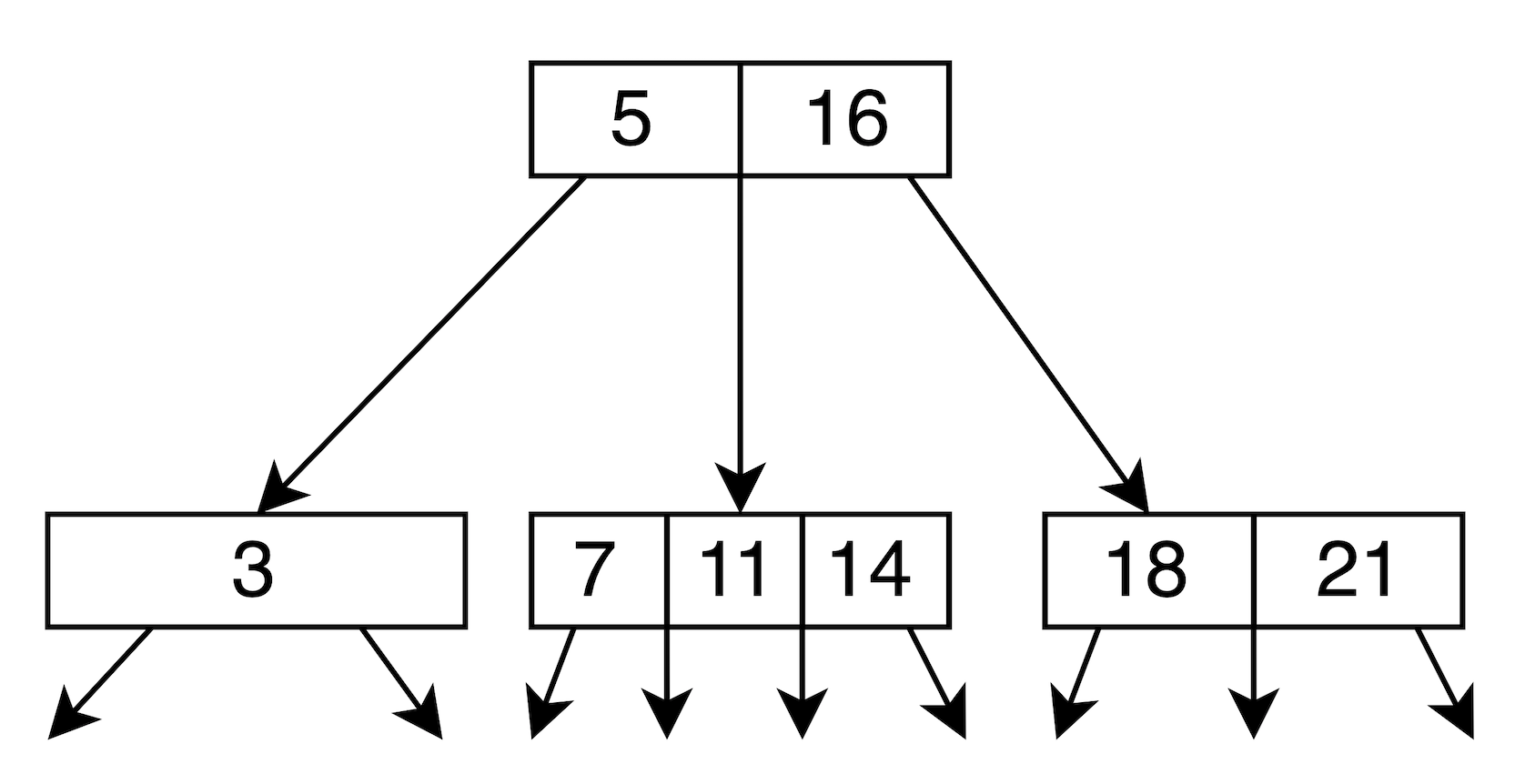
Example:

      5   |   16
     /    |     \
   3   7,11,14   18,21

2-3-4 Tree: Insertion

當要新增資料時:

  • directly insert: 還有空間

  • upper insert and split: node 的 element 已經滿了

    取所有元素的中間值，upper insert，
剩下的元素分家(split)，依照所選的中間值，分左右子節點。

Example:

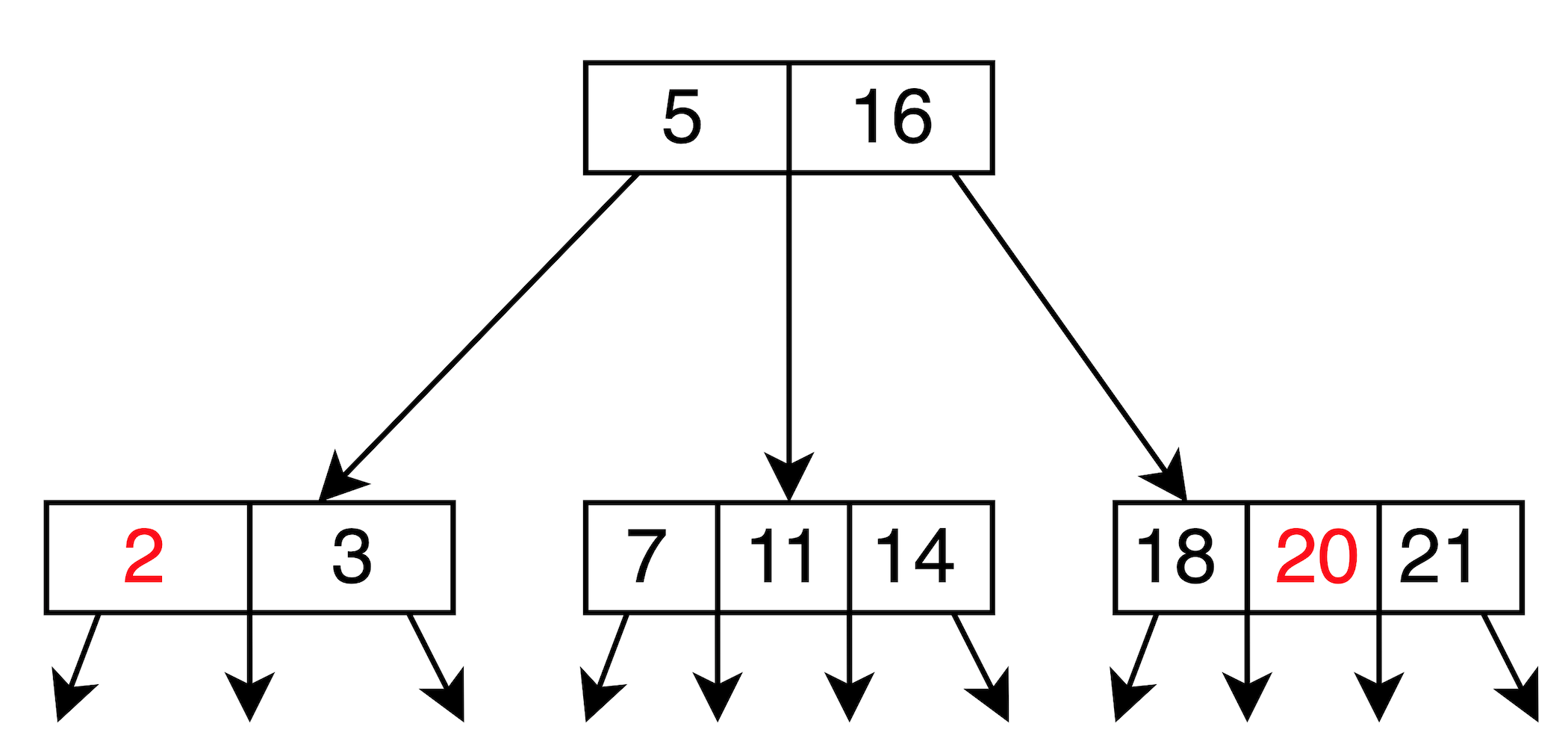
原本有一個 2-3-4 Tree 如下:

Step 1. insert 2 and 20

節點 element 尚未滿，所以 directly insert

Step 2. insert 13

節點的 element 已滿，所以 upper insert and split

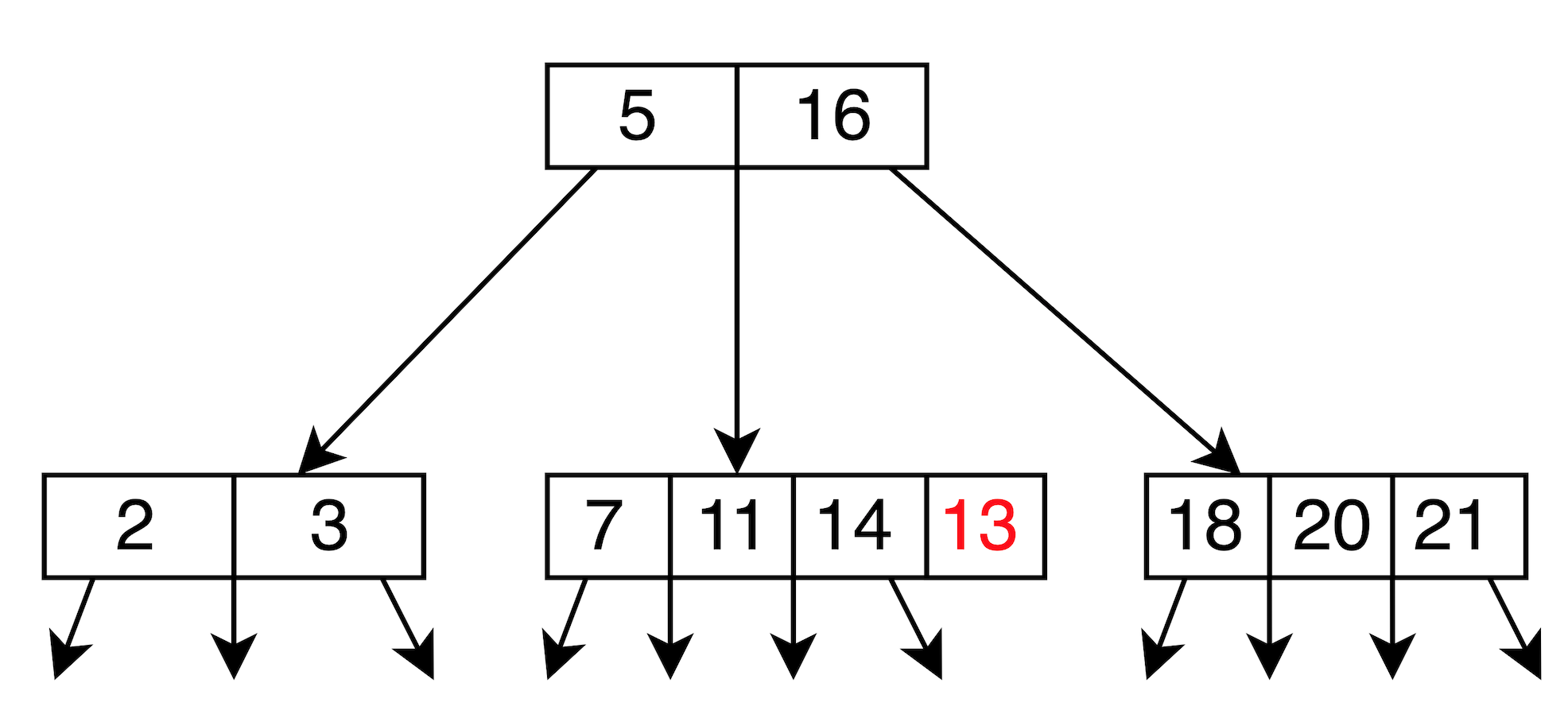
處理方式如下:

insert 13 -> [7, 11, 13, 14] -> Overflow!

upper insert and split: 選中間值 11

    11  <- upper insert
   /  \
  7   13, 14
   split

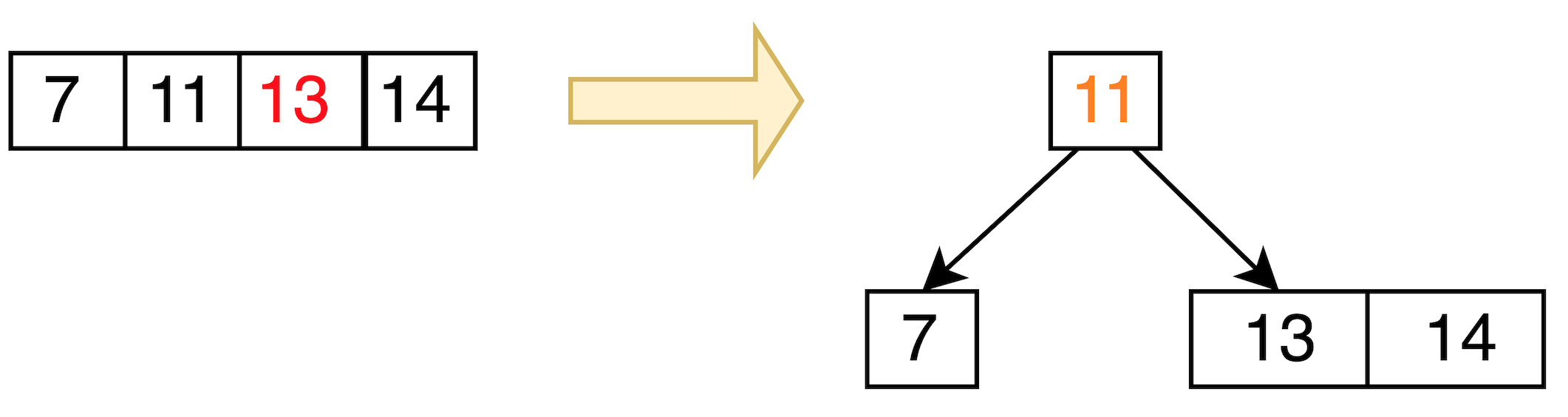
所以變成

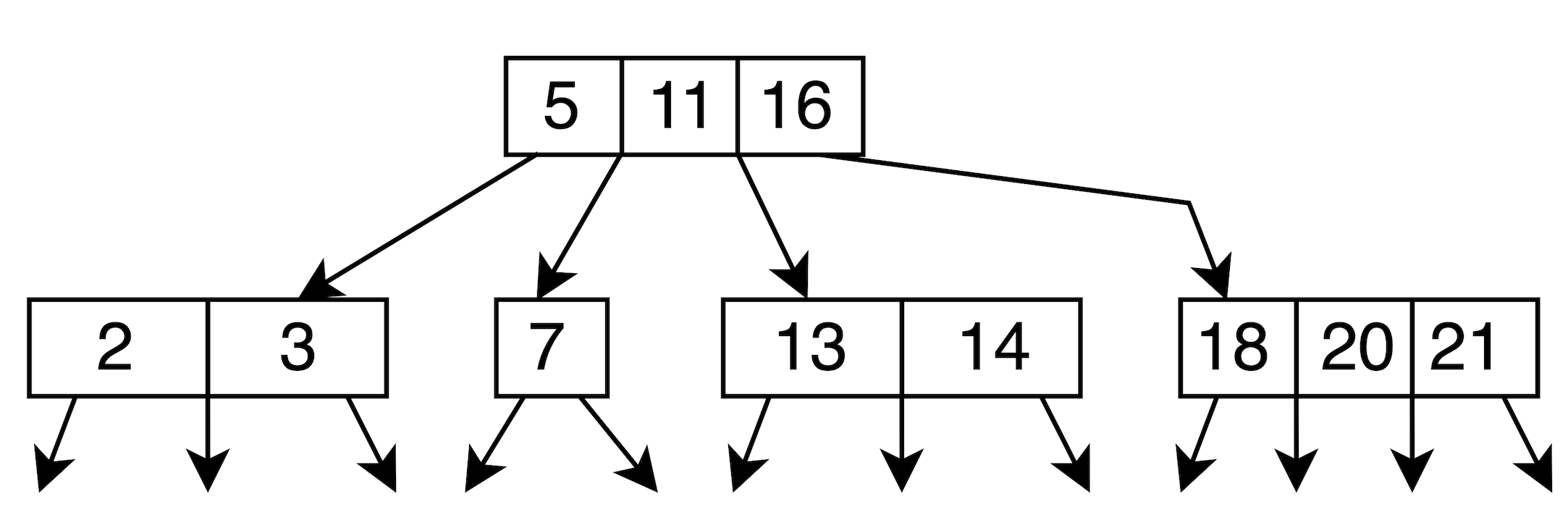
Step 3. insert 23

節點的 element 已滿，所以 upper insert and split

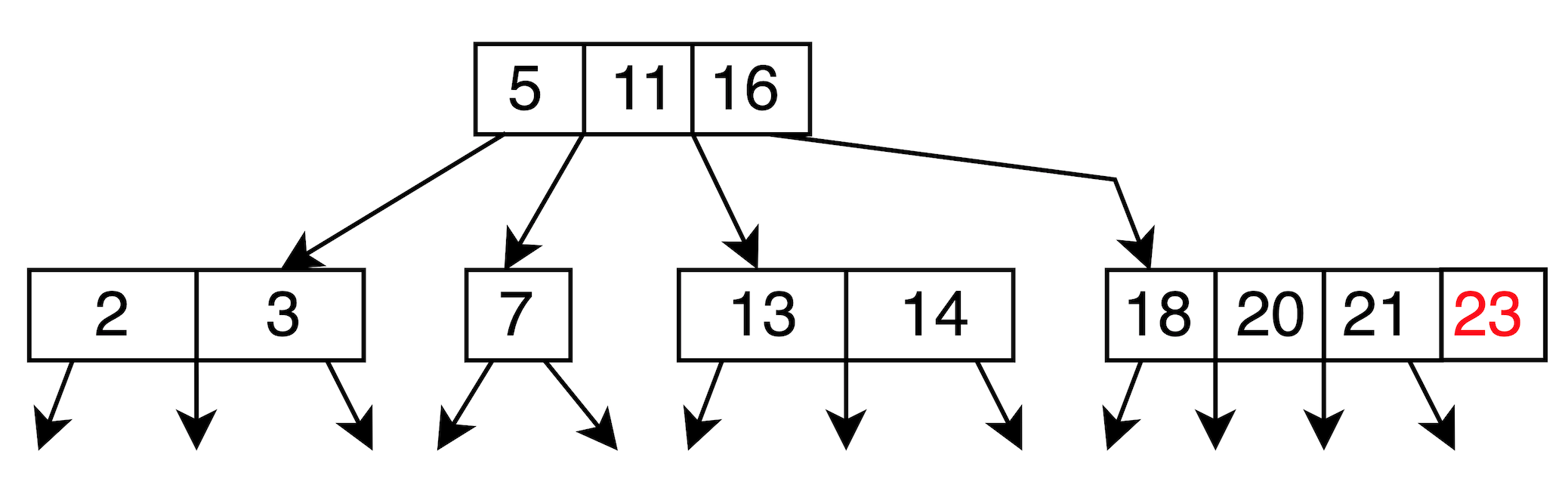
處理方式如下:

insert 23 -> [18, 20, 21, 23] -> Overflow!

upper inser and split: 選中間值 20

    20  <- upper insert
   /  \
  18   21, 23
   split

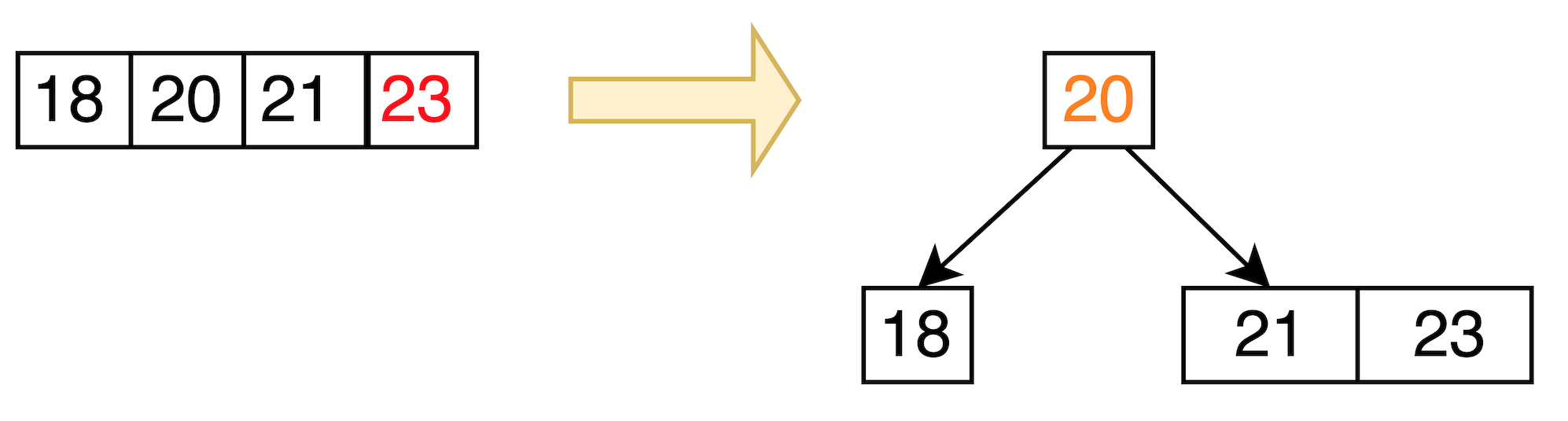
所以變成

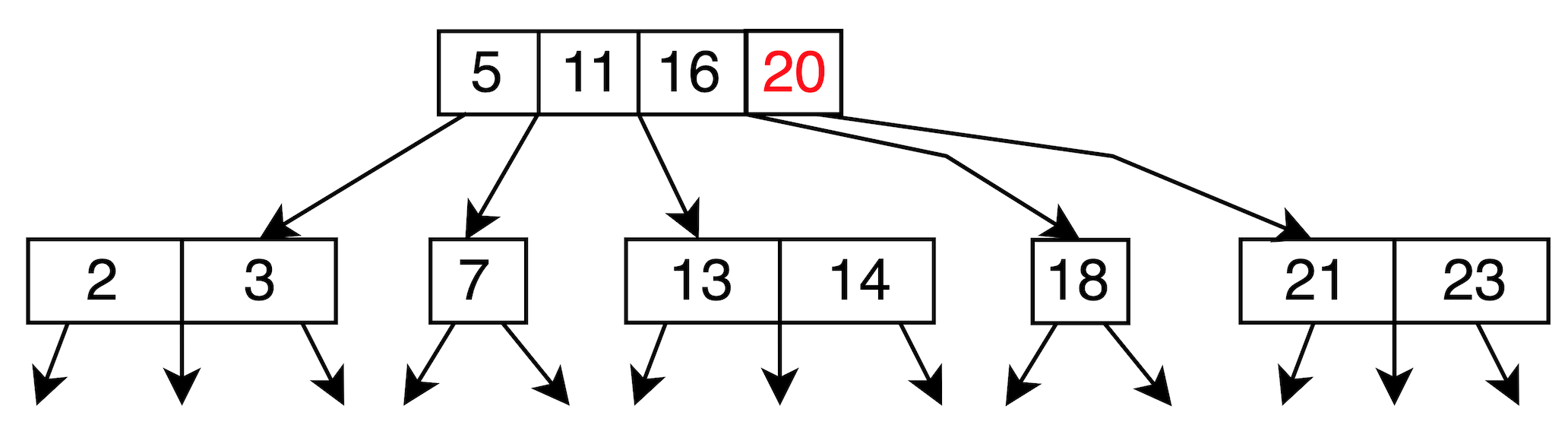
但此時發現上一層也發生 overflow: [5, 11, 16, 20]
所以再一次 upper inser and split: 選中間值 11

    11  <- upper insert
   /  \
  5   16, 20
   split

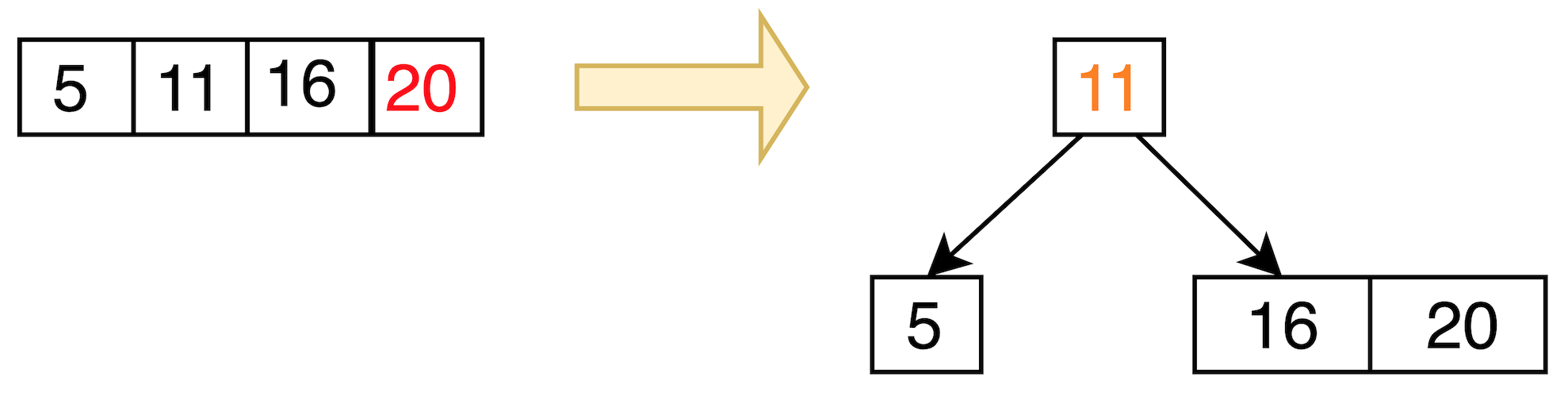
所以變成:

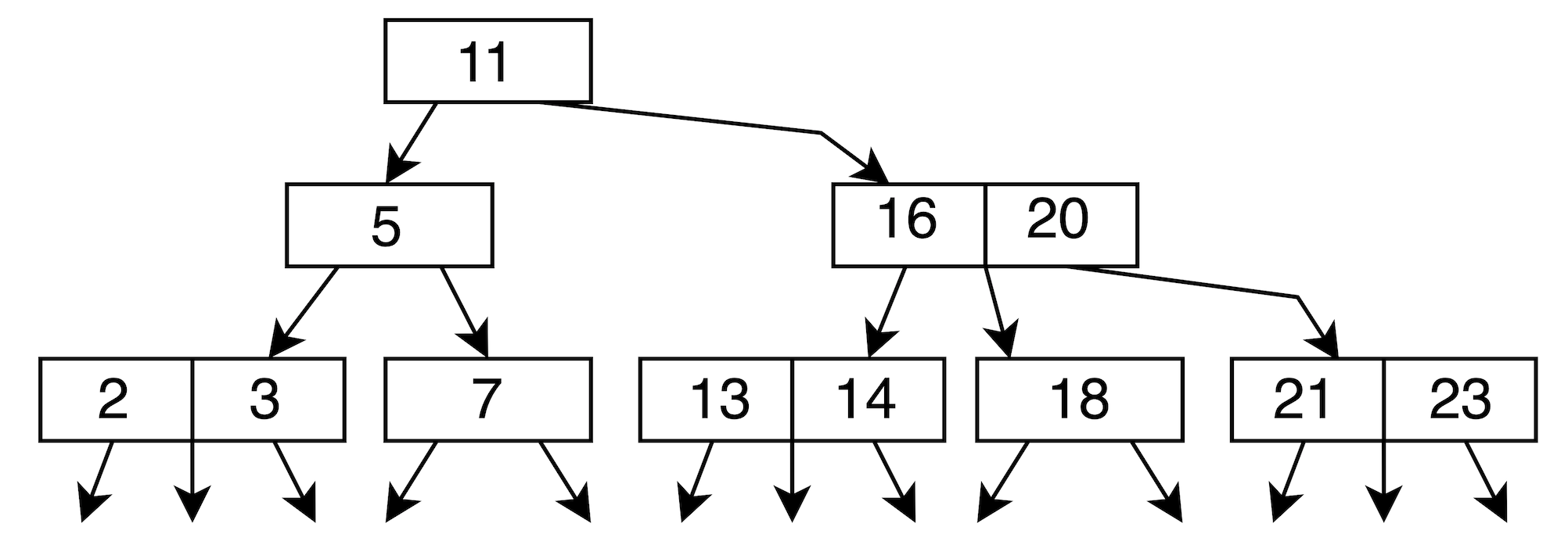
Exercise

1 ~ 10 依照順序插入 2-3-4 Tree，答案如下:

2-3-4 Tree: Removal

BST 重要概念: 我們希望 Removal 發生在 leaf node。

刪除節點有兩種: 刪除葉節點與刪除非葉節點。但我們希望 Removal 發生在 leaf node，因為從中間砍掉在組合回來是很麻煩的一件事。如下所示:

從上圖可知，我們想要刪除非葉節點，我們可以:

  • 將其左子樹中最大的點提上來補
  • 將其右子樹中最小的點提上來補
範例為 remove 3，然後 3 上去補 5 的位置。

於是我們可以將任何 remove node 改成 remove leaf node

且 Remove leaf 有三種情境:

  • Remove from 4-node: easy
  • Remove from 3-node: easy
  • Remove from 2-node: hard

1. Remove from 4-node: easy

直接移除即可。

如下所示:

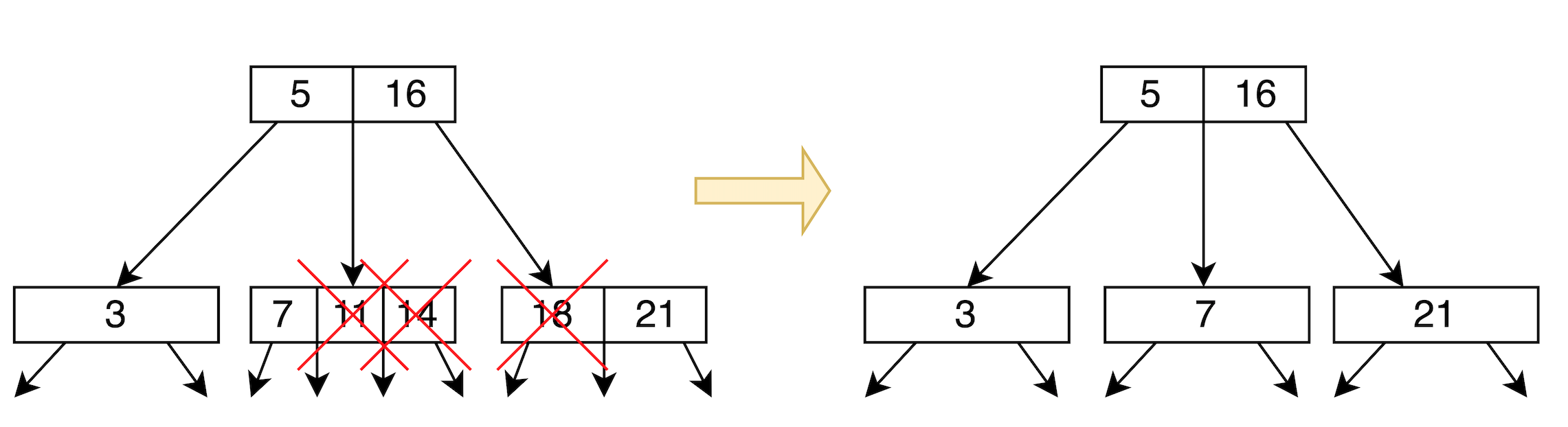
2. Remove from 3-node: easy

直接移除即可。

如下所示:

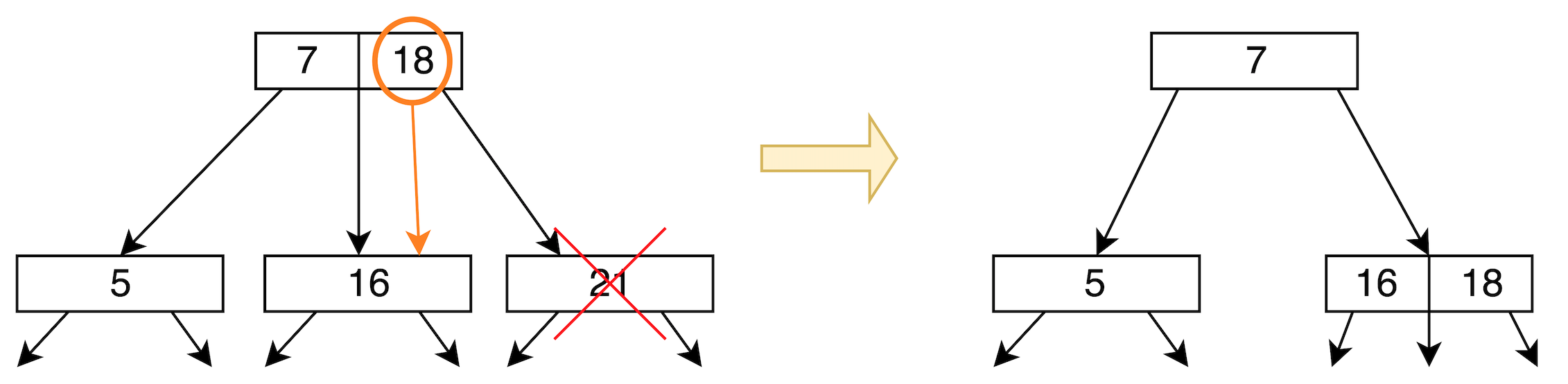
3. Remove from 2-node: hard

因為所有葉節點(leaf)皆在同一level 如果移掉的話高度就會不一樣!

此又可細分為兩種情境:

  1. Transfer: 隔壁家有人可以借

    Transfer when borrowable

    隔壁有人，從隔壁借人。

    Occur on 4-node and 3-node sibling

    如下所示:

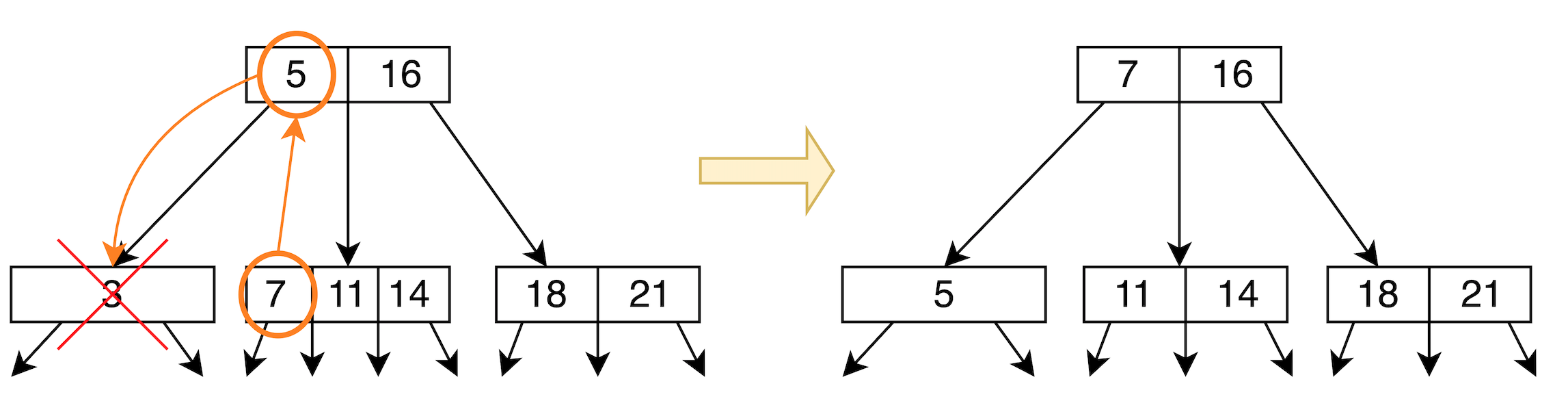
  2. Fuse: 隔壁家沒人可借

    Fuse and remove from upper level

    把上一層移掉，往下移。
把爸爸拉下來，跟兄弟合成一個新的家。

    Occur on 2-node sibling

    因為是把上層移掉，所以也會遇到 remove 4/3/2 node 的 case。

    如下所示:

Reference

Kaka LinSoftware Engineer

AIoT