[DSA] AVL Tree 介紹

    Data Structure and Algorithm   Data Structure and Algorithm   Tree  Comments

AVL Tree

是 Balanced BST 的一種實作方式

與2-3-4樹及紅黑樹的差異: rebalance almost immediately

Adelson-Velsky and Landis Tree (AVL Tree) is a Binary Search Tree (BST) such that:

  • The difference between the height of the left and right subtree is either -1, 0, or +1.

    公式: $|heighted(T_L) - heighted(T_R)| \leq 1$

    Balanced Factor (BF): 1, 0, -1

從上性質可得:

AVL Tree: BST + Balanced Binary Tree

實作 AVL Tree: Rebalancing (Rotation)

在遇到不平衡情況時，為維持樹的平衡，需要調整樹的節點，這邊稱為 Rotation。如下所示:

Example:

  1. 有三個點 3, 5, 8 (RR)

    3 BF: -2                             5
 \              AVL maintain        / \
  5 BF: -1     ==============>     3   8
   \
    8 BF: 0

  2. 有三個點 3, 5, 4 (RL)

        3 BF: -2                     3                          4
     \           rotate 4, 5      \      rotate 3, 4       / \
      5 BF: 1   ==============>    4    ==============>   3   5
     /                              \
    4 BF: 0                          5
  • Rotation 有個很重要的目的: rotation 前與後的樹的 in-order traversal 相同 。

插入 (Insertion)

1. Binary Search Trees 的 insertion
2. 向上檢查高度是否符合AVL限制。(算 BF)
3. 如果符合，結束。
4. 如果不符合，旋轉。
  • 如發現該節點的BF>1時，請往下找兩層，並根據這兩層的左右方向，進旋轉。且旋轉類型有四種:
    • LL型：當插入的點在該節點的左邊的左邊
    • RR型：當插入的點在該節點的右邊的右邊
    • LR型：當插入的點在該節點的左邊的右邊
    • RL型：當插入的點在該節點的右邊的左邊

RR型:當插入的點在該節點的右邊的右邊

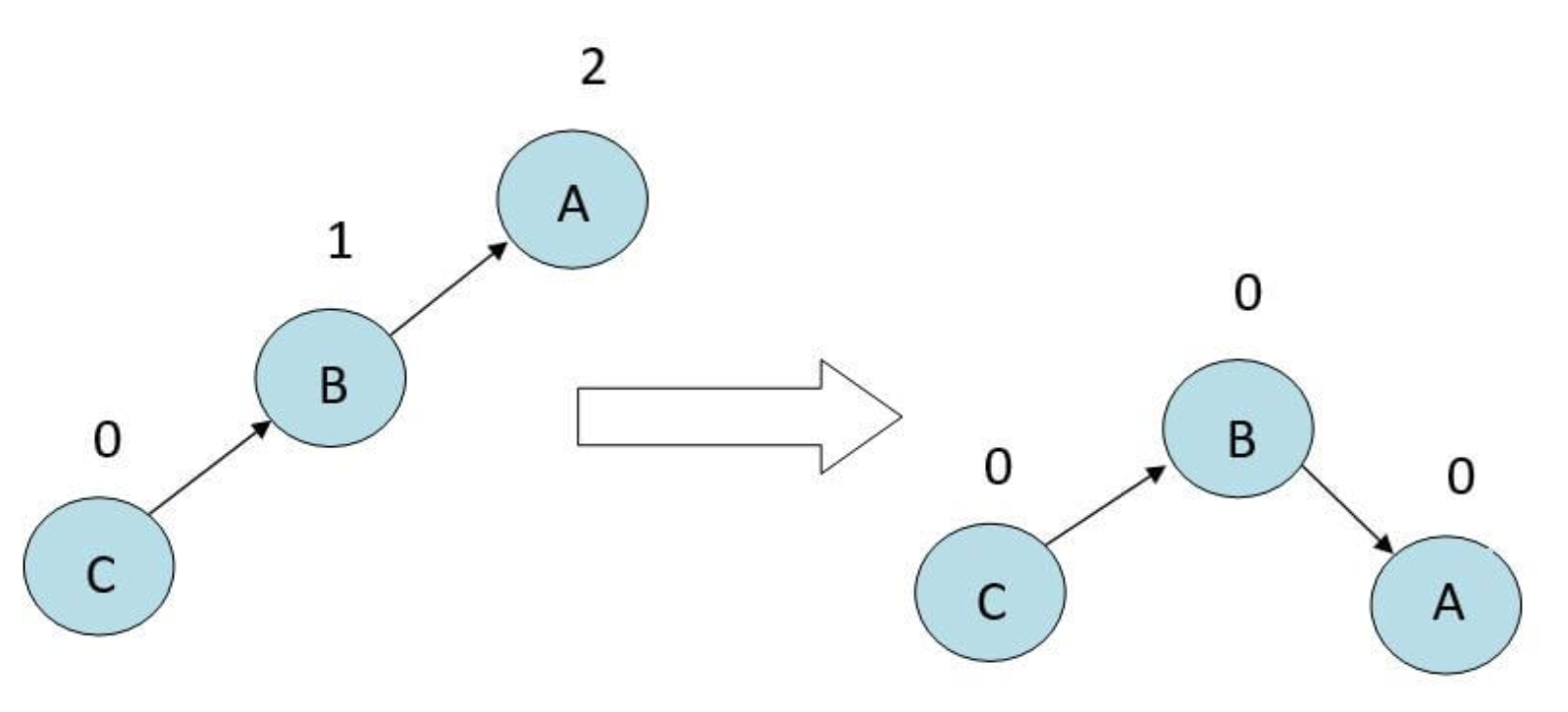
Rotating the node in the anti-clockwise direction.

“C” sub-tree 被新增到 “A” 的右節點的右節點。如下所示:

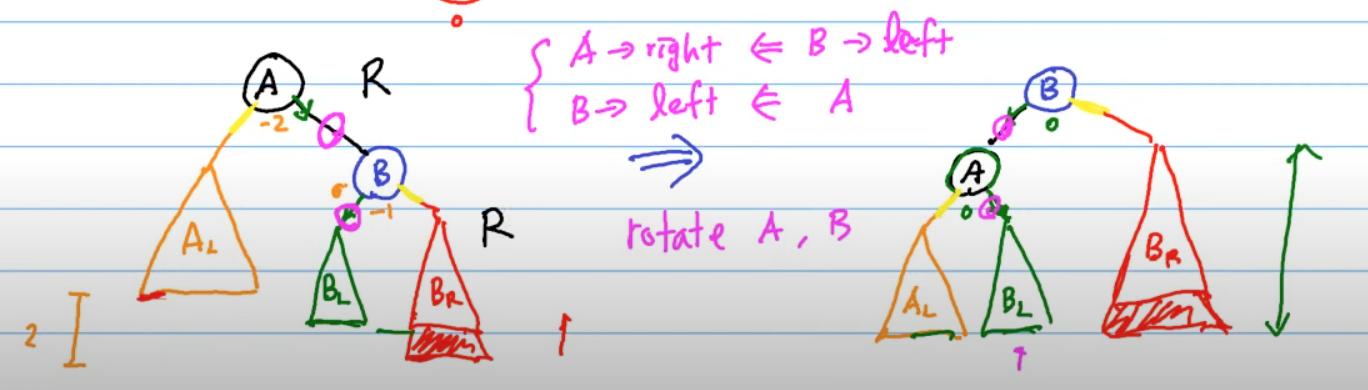
只跟 A, B 點有關，就是把 B 抓起來當頭，然後
- B 的左邊接 A
- A 的右邊接 B 的 左邊
  • 逆時針旋轉，B 變新的 root
    • B.left -> A
    • A.right -> B.left
*** 只要找到第一個不平衡的地方，調整完即可。 (一次調整)

LL型:當插入的點在該節點左邊的左邊

Rotating the node in the clockwise direction.

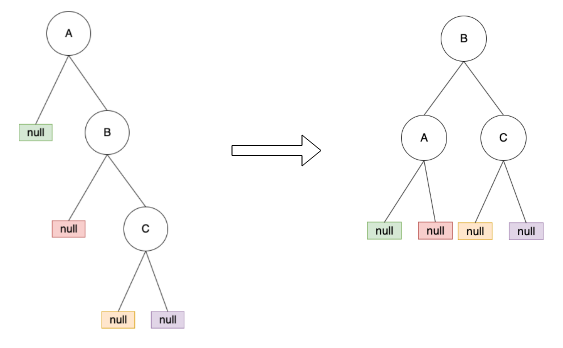
“C” sub-tree 被新增到 “A” 的左節點的左節點。如下所示:

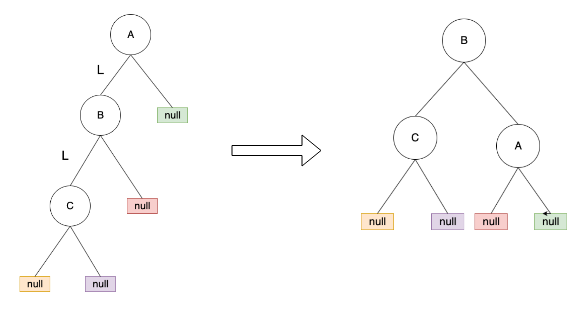
只跟 A, B 點有關，就是把 B 抓起來當頭，然後
- B 的右邊接 A
- A 的左邊接 B 的 右邊
  • 順時針旋轉，B 變新的 root
    • B.rigth -> A
    • A.left -> B.right
*** 只要找到第一個不平衡的地方，調整完即可。 (一次調整)

RL型:當插入的點在該節點的右邊的左邊

Right-left Rotation is the combination of RR rotation and LL rotation.

RL = RR + LL

所以我們:

  1. 先處理 susbtree 的 LL rotation
  2. 再處理 full tree 的 RR rotation

如下所示:

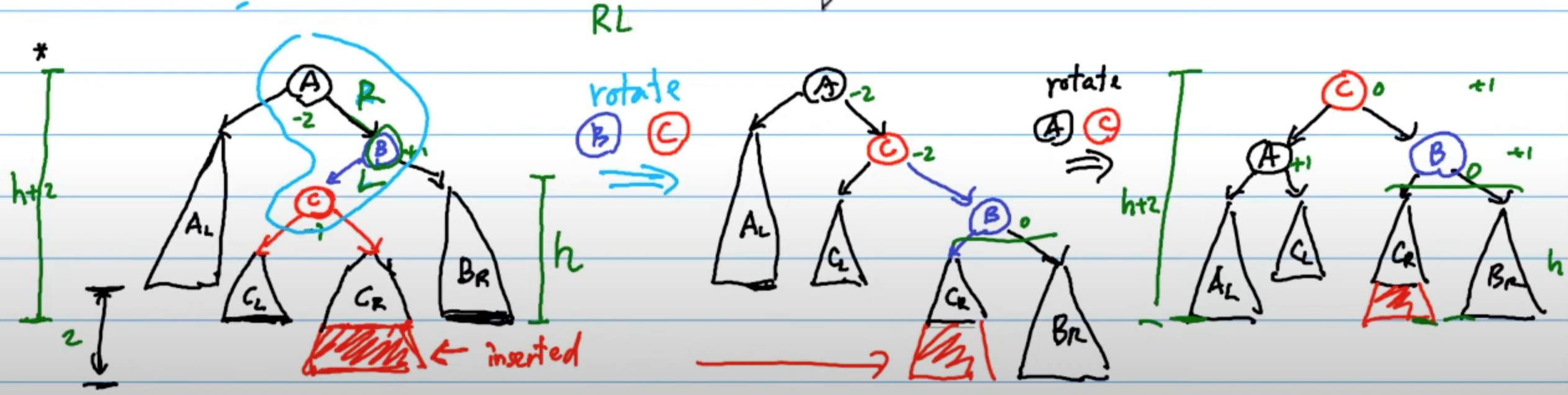
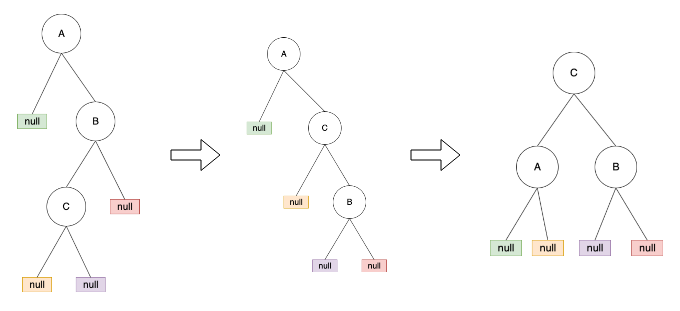
LR型:當插入的點在該節點的左邊的右邊

Right-left Rotation is the combination of LL rotation and RR rotation.

RL = LL + RR

所以我們:

  1. 先處理 susbtree 的 RR rotation
  2. 再處理 full tree 的 LL rotation

如下所示:

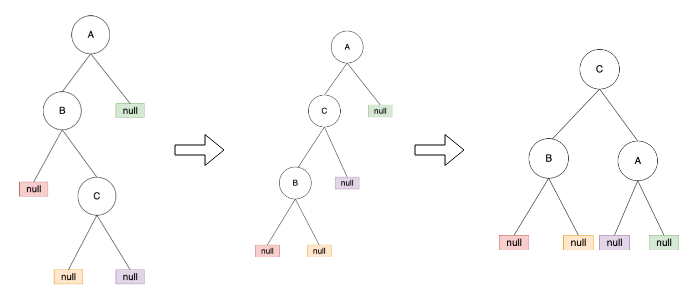
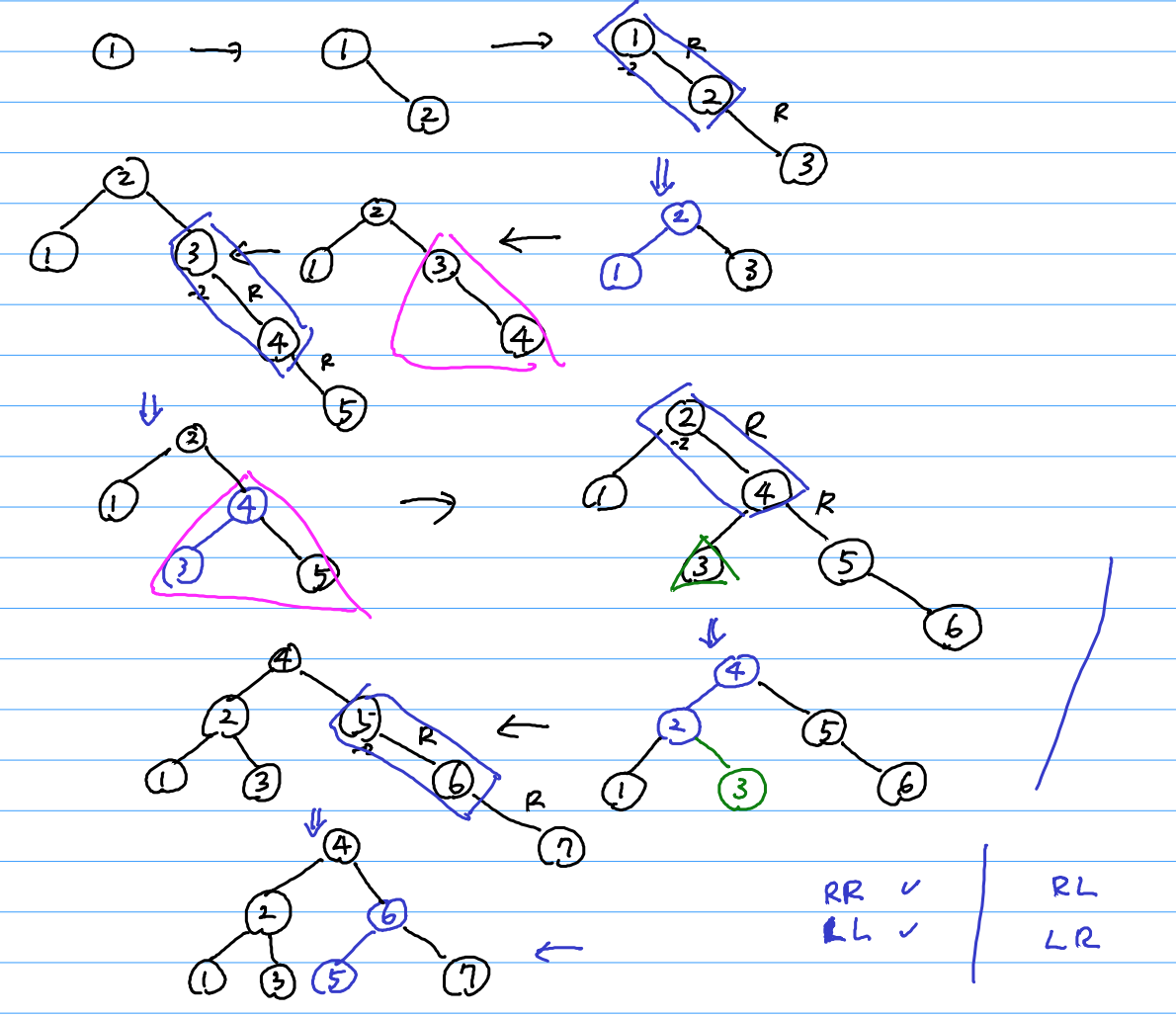
Example

  1. RR or LL

    data: {1, 2, 3, 4, 5, 6, 7}

Reference

Kaka LinSoftware Engineer

AIoT