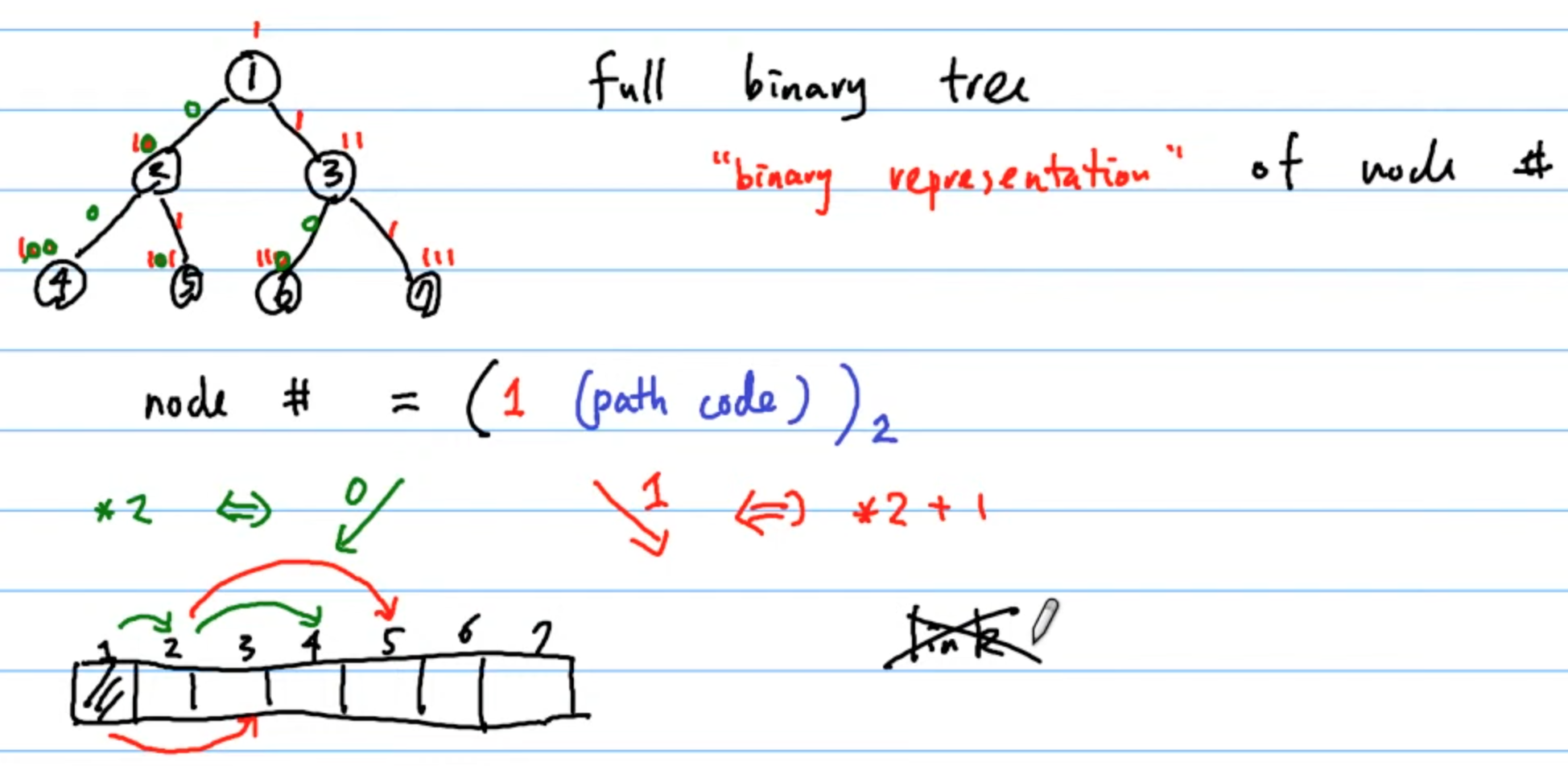[DSA] Binary Tree 介紹

    Data Structure and Algorithm   Data Structure and Algorithm   Tree  Comments

Binary Tree (二元樹)

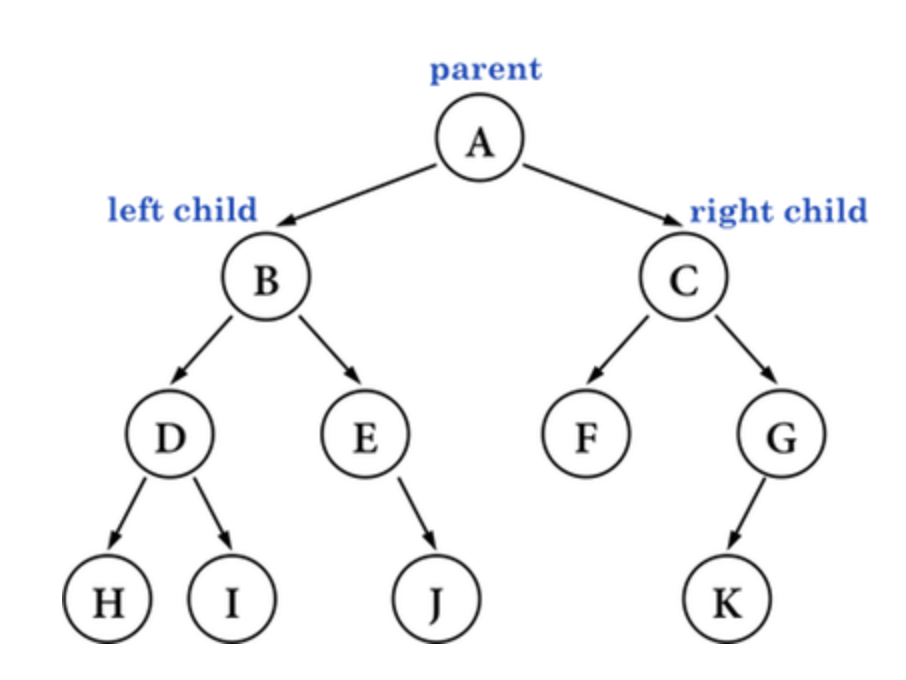
每個 node 最多就是只有 2 個 child node，且稱兩個 child node 為 left child 和 right child。

A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.

如下圖所示:

The height of the tree and amount of nodes

我們樹的高度與裡面能裝的node的數量有什麼關係？

在樹裡面我們在意的是某種程度的階層關係或是樹能長多高。從樹的高度會影響node的數量，這是很重要的，如: 現在有10萬筆資料，樹的最高與最矮差多少？

如下所示:

可得:

$$ h+1 \leq n \leq 2^{h+1} - 1 $$

假設今天是給定多少筆資料(n)，那今天樹的高度(h)是多少，如下:

$$ log_2(n+1) - 1 \leq h \leq n-1 $$

  • lg(n): binary search -> 好的

    樹很矮，很接近 lon(n) 的高度，可以找很快

  • n: sequence search -> 不好的

    樹很歪斜(skewed)，長得很像 Linked List
需花 linear 的力氣

在做 tree 相關 data structure 與演算法設計時 目標都是努力的壓低樹的高度 且讓每一層找的次數是一次或不要太多次 這樣 search 的效率就會接近 log(n) -> binary search

Types of Binary Trees

  • Full Binary Tree

    Every node has either 0 or 2 children.

    All nodes except leaf nodes have two children.

             1
      /     \
     2       3
    / \     / \
   4   5   6   7


         1
      /     \
     2       3
    / \
   4   5
      / \
     6   7


         1
      /     \
     2       3
    / \
   4   5
  / \
 6   7

  • Complete Binary Tree

    除了最後一層，其他層的節點全部填滿，並且最後一層必須是從左向右填，中間沒有空缺。

    All levels are filled with nodes except the last level, and in the last level, all the nodes are on the left side as possible.

             1
      /     \
     2       3
    / \     / \
   4   5   6   7

         1
      /     \
     2       3
    / \     / \
   4   5   6   7
  / \ /
 8  9 10

    a complete binary tree doesn’t have to be a full binary tree.

  • Perfect Binary Tree

    各層節點全滿。同時也是 full binary tree 和 complete binary tree 。

    All internal nodes have two children and all leaf nodes are at the same depth or same level.

             1
      /     \
     2       3
    / \     / \
   4   5   6   7

         1
      /     \
     2       3

  • Balanced Binary Tree

    每個 node 的左子樹和右子樹的高度差為 0 or 1。

    • It is a type of binary tree in which the difference between the height of the left and the right subtree for each node is either 0 or 1.

    • For each node, its left subtree is balanced

    • For each node, its right subtree is balanced.

                1
       /     \
      2       3
     / \
    4   5

      ***Unbalance

              1
     /     \
    2       3
   / \
  4   5
 /
6

    A binary tree is balanced if the height of the tree is O(Log n) where n is the number of nodes

  • Degenerate or Pathological Tree

    A Tree where every internal node has one child. Such trees are performance-wise same as linked list.

           1
      /
     2
      \
       3
      /
     4

  • Skewed Binary Tree (歪斜樹)

    A skewed binary tree is a pathological/degenerate tree in which the tree is either dominated by the left nodes or the right nodes. Thus, there are two types of skewed binary tree:

    • left-skewed binary tree (左歪斜樹): 一顆樹完全都往左邊長

             1
      /
     2
    /
   3
  /
 4

    • right-skewed binary tree (右歪斜樹): 一顆樹完全都往右邊長

       1
  \
   2
    \
     3
      \
       4

Binary representation of node number

Consider a Perfect Binary Tree or Completed Binary Tree:

             1
          /     \
         2       3
        / \     / \
       4   5   6   7

二進制為:

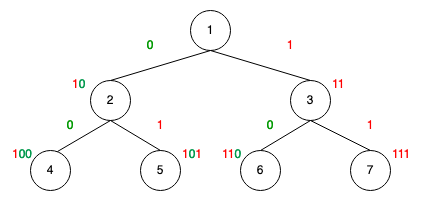
從上可知:

  • node number = (1 (path code)) 的 2 進制

    • 在一個二進位制後面加一個 0 : 就是 *2

      110: 6
1100: 12

      C 語言中就是 shift 一個 bit

    • 在一個二進位制後面加一個 1 : 就是 *2+1

      110: 6
1101: 13

最喜歡使用編號的 data structure 為 Vector， 所以我們可以用一個 Vector 來表示這個特別的 full binary tree，如下圖所示:

Reference

Kaka LinSoftware Engineer

AIoT