Binomial Heap

前言: 均攤 (Amortization) 介紹

在開始介紹 Binomial Heap 前，我們先來看看 Heap (Min Heap or Max Heap) 的 operation 時間複雜度:

• insert: O(log n)
• remove/delete: O(log n)

思考: 我們能不能減少 insert 的時間複雜度 -> O(1)，但一樣保持很快的 remove？

Ans:

hard if every operation O(1)
possible if "amortized (均攤)" O(1)

• amortized(均攤):

  有時候花多一些時間，有時候花少一些時間，平均起來會是固定的時間

  example: Dynamic Array (extendable)

Amortized on Heap Tree

• Cheap insertion usually:

  insert to “small tree” usually

• Expensive insertion sometimes:

  insert to “big tree” sometimes

這邊就有小樹跟大樹同時存在。一個 data structure 有很多棵樹就稱為 Forest (森林)。

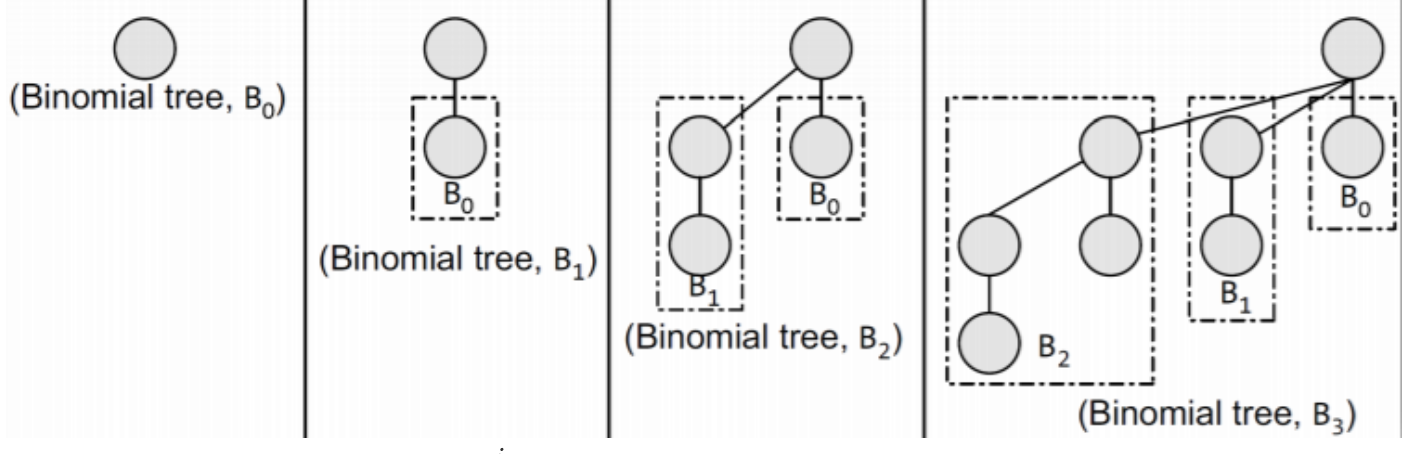
Binomial Tree (二項式樹)

Binomial Tree 定義如下:

• A binomial tree of order 0 is a single node
• A binomial tree of order k has a root node whose children are roots of binomial trees of orders k-1, k-2, …, 2, 1, 0 (in this order).

如下圖所示:

圖片來源: Url

由上圖我們可以得知:

• $B^k$ node 數: $2^K$ nodes
• $B^k$ 高度為: k
• Degree of root: k

Binomial Heap (二項式堆積)

Binomial Heap 就是由 Binomial Tree 組合而且， 且每一個 Binomial Tree 都是 Heap Tree。

Binomial Heap is a collection of binomial trees, and each binomial tree is heap tree.

Example:

• n = 10: 8 (B3) + 2 (B1)
• n = 13: 8 (B3) + 4 (B2) + 1 (B0)

如下圖所示，以下用 Max Heap 舉例:

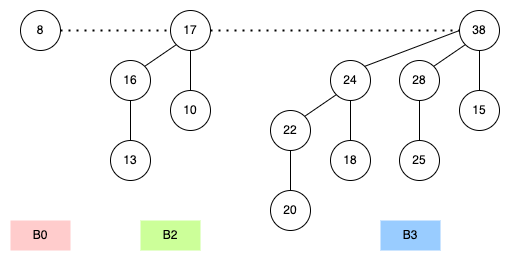
Example of a binomial heap containing 13 nodes. The heap consists of three binomial trees with orders 0, 2, and 3.

Binomial Heap: Sequence of Inserts

現在來看一下如何插入 node 到 Binomial Heap 裡， 假設現在有一個空的 Binomial Heap，如下:

binomial heap: {}

Step 1.
  insert 5 into {} => { B0 }

  => { 5 }

Step 2.
  insert 7 into { 5 } => { B1 }

  *** 7 也是一個小的 binomal heap { B0 }
     => merger { B0, B0 } => { B1 }

  =>  7
      |
      5

Step 3.
  insert 3 into { B1 } => { B0, B1}

  => 3, 7
        |
        5

Step 4.
  insert 2 into { B0, B1 } => { B2 }

  => merge { B0, B0 } to { B1 }, merge { B1, B1 } to { B2 }

  => 3  7    =>      7
     |  |          / |
     2  5         3  5
                  |
                  2

由上可知, insert N nodes 時:

1. erevry one insertation: add B0, O(n)
2. 每 2 輪要 merge { B0, B0 }, n/2
3. 每 4 輪要 merge { B1, B1 }, n/4
4. 每 8 輪要 merge { B2, B2 }, n/8

After n insertions (insert + merge):

$$ \frac{n}{2^k} + \frac{n}{2^{k-1}} + \frac{n}{2^{k-2}} + … + n = O(n) $$

• time complexity: O(n), amortized O(1)

Find Maxmum/Minimum

• time complexity: O(log n)

Delete Maxmum/Minimum

• time complexity: O(log n)

Reference

• DSA 20200505: Heap/Hash Table
• wiki: Binomial heap
• [資料結構] CH19. Heaps