Heap Tree

用 Tree 了解他，用 Array 實作相關的 operation

從 Binray Tree 的觀念出發，首先將原本 Tree 的 node 加上 Key (檢索鍵)，如下:

• key: priority or weights or others
• data: original data (like: todo)

有分:

• Min Heap(最小堆積):

  A min heap is a complete binary tree that is also a min tree.

• Max Heap(最大堆積):

  A max heap is a complete binary tree that is also a max tree.

  又稱 complete binary max tree)

概念類似 priority queue (heap on array)。

以下假設為沒有 priority queue 的年代， 用 Tree 的特性來設計 priority queue。

設計思路

• 需求: 最大的 Key 可以很快被找到
• 限制: 使用 Binary Tree 來實現
• 目標: Max Heap / priority queue, 降序 descending)

可簡單分為3個步驟1個限制:

1. 把最大的放在 root
2. 如何很快的找到下一個最大的值 (繼承人)

這兩步驟為第一步的設計，又被稱為binary max tree。

3. 用 Complete Binary Tree 來壓 tree 的高度

• 限制: 先維持 complete binary tree 的性質

要求 tree 的長相，稱為 complete binary max tree

各步驟詳細如下面介紹。

1. 把最大的放在 root

想法: 就直接把 Key 最大的放在 root。如下圖:

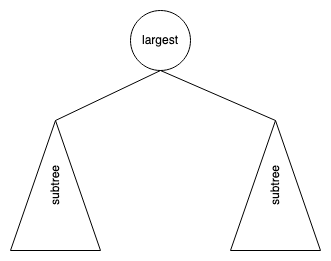
Exmaple:

      14
    /    \
   6      8
  / \    / \
 12  5  7   9

問題: 當把目前最大的 14 拿到後，需 traversal 剩下的所有 node 後，才能得到下一個最大的 node: 12

=> 超花時間

2. 如何很快的找到下一個最大的值 (繼承人)

Subtree 的 root 也都分別各自 subtree 中最大的 (sub-largest)，如下圖:

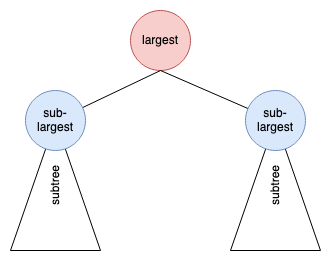
當 largest 被拿走後，就是兩個 subtree 的 sub-largest 比較一下就知道下一個是誰要補位上去。

Example:

      14
    /    \
   12     9
  / \    / \
 6  5   7   8

Binary Max Tree

上面兩步驟為第一步的設計，其又被稱為binary max tree。

• root key >= other node's key
• every subtree is binary max tree

操作步驟如下:

      14
    /    \
   12     9
  / \    / \
 6   5  7   8

1. Get Largest: root, 14

2. Remove Largest and get sub-largest

   12 跟 9 比大小，但因為 12 補上去了， 他的那個 subtree 也要再補一個 sub-largest

   => 6 跟 5 比較，6上去補位

      12
    /    \
   6      9
    \    / \
     5  7   8

如此循環下去。

replace with largest of sub-root recursively

Worst time complexity

如果遇到 tree 是 skewed binary tree (歪斜樹) 時，

• time complexity O(h): O(n)

   50
  /
 48
  \
   30
  /
 21
  \
   10
   /
  3

binary max tree maintain 時要花很大力氣。

下一個思考思路就是:

-> 壓低 tree，讓 time complexity O(h) 從 O(n) 變為 O(log n)

3. 用 Complete Binary Tree 來壓 tree 的高度

要求 tree 的長相，稱為 complete binary max tree

不用 perfect (full) binary tree 的原因是因為 node 數量都是奇數

我們要如合結合 complete binary tree 與 binary max tree 呢？

Example:

      14
    /    \
   12     9
  / \    /
 4   8  5

1. Get Largest: root, 14

2. Remove Largest and get sub-largest

   12 跟 9 比大小，但因為 12 補上去了， 他的那個 subtree 也要再補一個 sub-largest

   => 8 跟 4 比較，8上去補位

      12
    /    \
   8     9
  /     /
 4     5

Note: 可能會想說把 5 往左移。但如果不是 5 是 8.5 呢？

這樣變成不是 complete binary tree 了， 事情變麻煩了，不好做。

換個思路思考!

先維持 complete binary tree 的性質

缺位時，先維持 complete binary tree 的性質

當 remove node 時，先讓最尾把的 node 補上來

=> 維持 complete binary tree

然後再讓 root 去跟 sub-largest 去比。

Example:

      14
    /    \
   12     9
  / \    /
 4   8  8.5

先讓最尾把的 node 補上來:

      8.5
    /    \
   12     9
  / \
 4   8

然後再去跟 sub-largest 比:

      12
    /    \
   8.5    9
  / \
 4   8

然後 8.5 再去跟他的 sub-tree 去比，如此循環。

結論

Complete binary max tree 就是一般所稱的 Max Heap。

操作步驟如下:

Remove:
   1. move last node to root (complete binary tree)
   2. sink down to keep binary max tree
        time complexity: O(log n)

Insertion node

如果要新增 node，一樣先插在最後面，維持 complete binary tree，再去檢查 binary max tree 性質。

insertion:
   1. insert at last (com plete binary tree)
   2. floot up to keep binary max tree
        time complexity: O(log n)

範例如下，插入 node 17:

1. 放在最後面，維持 complete binary tree

      14
    /    \
   12     9
  / \    /  \
 4   8  8.5  17

2. 逐項比大小，維持 binary max tree 性質

      14
    /    \
   12     17
  / \    /  \
 4   8  8.5  9

      17
    /    \
   12     14
  / \    /  \
 4   8  8.5  9

Heap v.s Array

• Complete binary tree -> array

• Heap tree -> partially ordered array

        14
      /    \
     12     9   -> 14, 12, 9, 4, 8, 8.5
    /  \   /
   4    8 8.5
  

Heap sort

假設已經有 array 與 heap

• select sort on array: O(n^2)

  n^2: O(n)次 * O(n)找
  

• select sort on heap: O(n*log n)

  n*log n: O(n)次 * O(1)找 + O(log n)排
  

那建好一個 heap 要花多少力氣？

利用 insertion 建立 heap
建立力氣: O(n)insertion * O(log n) -> O(nlog n)

所以:

1. 從 unordered arry 變成 heap: O(nlog n)
2. 再從 heap 去 sort: O(nlog n)

Heap sort time complexity: O(nlog n)

Reference

• DSA 20200421: Tree/Heap