[DSA] Hash Table 介紹

    Data Structure and Algorithm   Data Structure and Algorithm   Hash Table  Comments

Hash Table

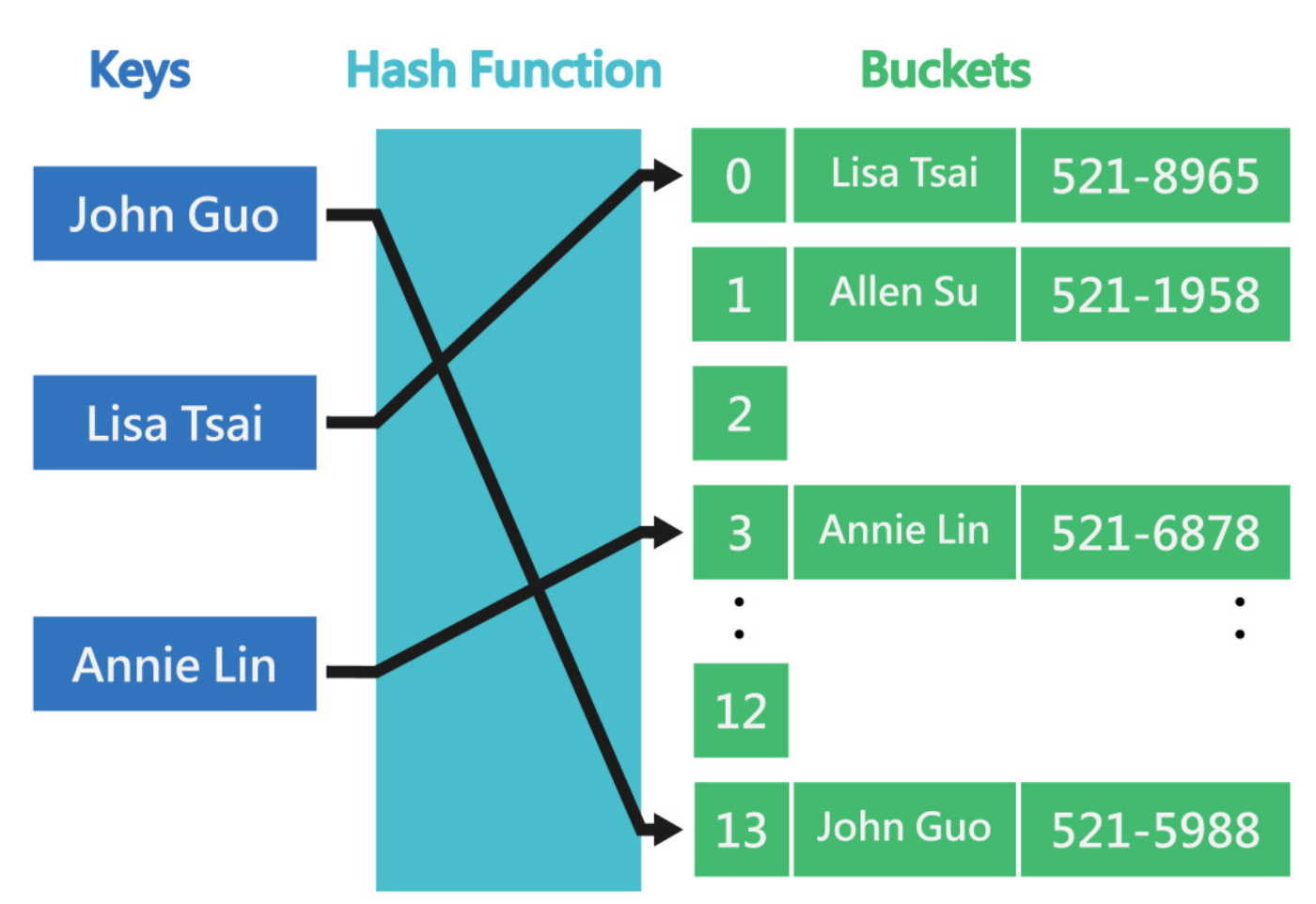
Hash Table 就是儲存 (key, value) 這種 mapping 關係的一種資料結構。 它是透過 Hash Function 來計算出 key 與 value 所對應的位置，如下所示:

前言

在 prority queue 裡，我們在乎的是資料的大小(優先度)， 但今天我們不是在乎大小(優先度)，而是根據給定的 key 去做相應的處理，那我們就稱其為 map or dictionary。

  • map:

    { key: value }

    example:

    key1: value1
key2: value2

  • dictionary: { key, set(value) }

    { key:  set(value) }

    example:

    key1: value1,1
      value1,2
      vaule1,3
key2: value2,1
      value2,2
      vaule2,3

Implement Hash Table data structure

在開始實作 Hash Table 前，我們先思考一下有沒有已經有的data structure 可以實作出相同的特性，以 map 來思考。

思考出發點: Using Array as Map

  • Thinking 1. 假設 key 是 integer (small)

    • key as array index
    • value as array data
      insertget
      O(1)O(1)

  • Thinking 2. 假設 key 是很大的 integer

    需要很大的 array，很浪費空間。

  • Thinking 3. 壓縮 key

    壓縮空間，如:

    將 10000 種 key 至空間大小為 100 的 array 內

  • Thinking 4. key 不是 integer 時

    假設 key 不是 integer，而是 string 時， 我們就需要 conver string to integer。

結論

  • 快速的 convert (convert to integer)
  • 快速的 壓縮 key (small integer)
  • 快速的 array operate

就可以達到快速的 map 的 implementation。

專有名詞介紹

Example:

insert (key, value) => A[h(key)] = value
get value by key => value = A[h(key)]
                            / \
                Bucket array  hash function

  • 桶(Bucket array):

    雜湊表中儲存資料的位置，每一個位置對應唯一位址(Bucket Address)。

  • perferc hashing: key 一對一的對應到一樣數量的數字。

                  1-1                   99
{100 key}   <-----> {0, 1, 2, ..., K-1}

  • 碰撞(Collision):

    若2筆資料經過雜湊函數運算後的雜湊值相同，也就是對應到相同位址時，稱為碰撞。

hash 困難點: > - 找出好的 hash function > - 處理 collision 問題

Hash Function (雜湊演算法)

Hash function: hash code + compress

是一種從任何一種資料中建立小的數字「指紋」的方法。雜湊函式把訊息或資料壓縮成摘要，使得資料量變小，將資料的格式固定下來。如下所示:

h: key                           small integer
    |                                  |
    |  hash code             compress  |
    |-------------> integer ---------->|

Example of hash function and collision

Key: str，假設:

hashCode(str) = str[0] - 'a' (ascii)
compress  = hashCode(str) % K

Then

hashcode("apple") = hashcode("act")

常見的 Hash Function

Hash Code

  1. Summation: Σ key[i]

    • 優點: 計算快速

    • 缺點: 對位置(position)不敏感

      "abc" = "acb"

  2. Polynomial: Σ key[i] * A^i

    Σ key[i] * 16^i -> shift, bit 運算

  3. Cyclic shift: shift後，溢位的部份補回低位數

Compress

  1. 除法(Mod/Division):

    相除取餘數來當作雜湊值。例如:

    有 11 個 Bucket，若有數值4。
=> 4 mod 11 = 4，雜湊值為4。

Collision handling

雜湊表初始的陣列規模若太小，容易造成碰撞次數增加，而需要多次的碰撞處理; 若規模太大，容易造成過多未儲存數據的陣列空間，因此初始設定適當的陣列規模相當重要

0. Don’t care

  • throw away
  • don’t insert

tolerate some errors

Example: hash-based map, set()

set() = {k1, k2, …, kp}

bit bucket array

[0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1]

a[h(k1)] = 1
a[h(k2)] = 1
a[h(kp)] = 1
  1. 當 a[h(ki)] = 0 時, 此 key 沒在 set() 裡:
    • no error
  2. 當 a[h(ki)] = 1 時, 此 key 在 set() 裡:
    • correct if no collision
    • ? if collision

**** Advance data structure: bloom filter

1. Fixed array per bucket

Can still overflow

2. Linked list per bucket

Known as Chaining.

hope short chain

4. Reuse empty space (Open addressing)

有一個最想放入的 bucket，但有人了，嘗試放置接近的 bucket

Example:

進教室找位置時，發現自己想要的位置被座時
就找第二、第三等等的位置，嘗試 N 次後就放棄

Steps for insert:

  • insert (key, value) to array location h0(key)
  • if fail, re-insert to h1(key)
  • if fail, re-insert to h2(key)
  • if fail, re-insert to hm-1(key) [嘗試 m 次]
  • declare failure

Get value 一樣流程

那如何定義 h0, h1, h2, …, hm-1 呢？

  1. 線性探測法(Linear Probing)

    將以線性方式往後尋找直到有空的Bucket為止，一般來說也會視為環狀結構，若後面Bucket都滿了，可以循環到前面尋找。如下:

    $h_i = (h_{i-1} + 1) % K = (h_0 + i) % K$

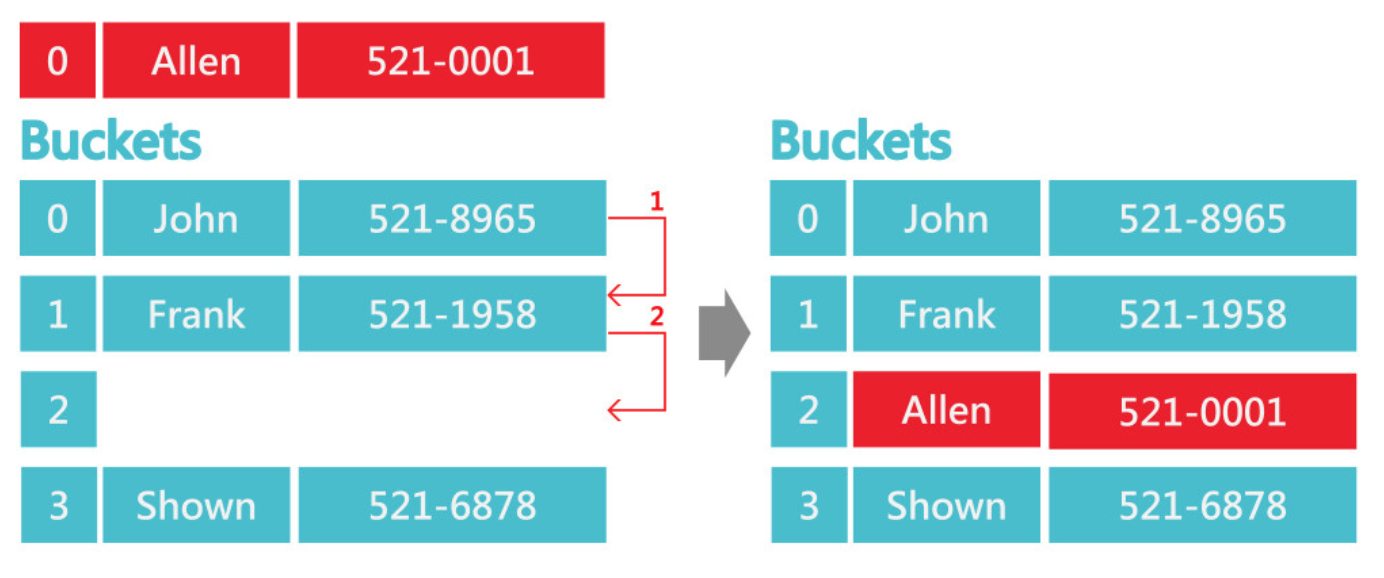
    最多就是找遍整個 array: m at most K-1

  2. 平方探測法(Quadratic Probing)

    $h_i = (h_0 + i^2) % K$

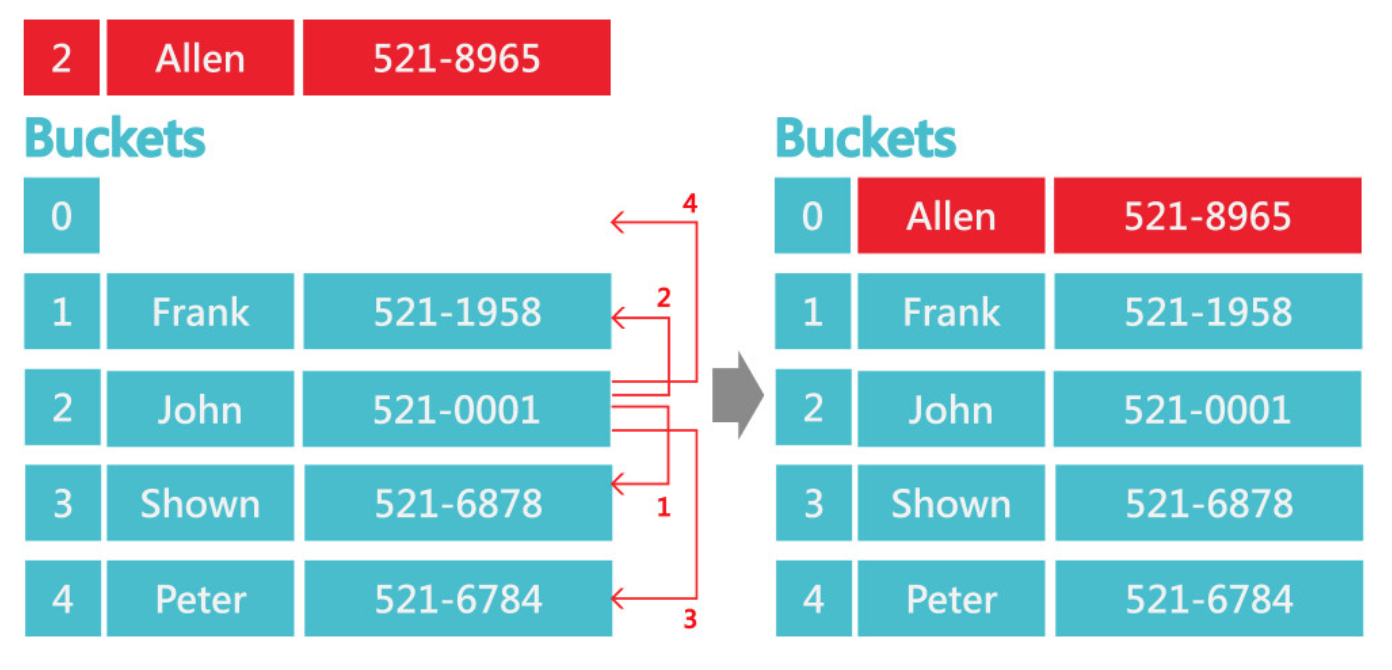
  3. double hashing

    $h_i = (h_0 + i * \hat{h}(key)) % K$

5. Extendable Hash Table

當我們的資料越來越大時，碰撞的機率也會大大增加， 這時候可以考慮擴增 Hash table。

有兩種方法，如下:

  • naive (rebuild all):

    1. set new_K = 2K
    2. h(key) change range to { 0, 1, …, 2K-1 }
    3. rebuild

  • partial rebuild:

    Example:

    h(key) = (key[0] - 'a') % K

Origin Table:       insert "egg"

{
 0: "act", "eat"
 1: "bird"
 2: "good", "cat"
 3: "dog"
}

變大兩倍，把 "eat", "egg" 放到新位置，
但是 "good" hash code 會變 6，
所以把尚未分家的與新家連上一個小紙條 (1-5, 2-6, 3-7)
當 "good" 那邊 overflow 時在分家處理

{
 0: "act"
 1: "bird"
 2: "good", "cat"
 3: "dog"
 4: "eat", "egg"
 5:
 6:
 7:
}

Reference

Kaka LinSoftware Engineer

AIoT