Segmentation Metrics
影像分割是對影像中的每個 Pixel 做分類,可分為:
- 語意分割 (Semantic Segmentation): 注重類別之間的區分,而不是同類別不同個體
- 實例分割 (Instance Segmentation): 同時注重類別及同類別中不同個體
- 全景分割 (Panoptic Segmentation): 語意分割+實例分割。
如下所示:


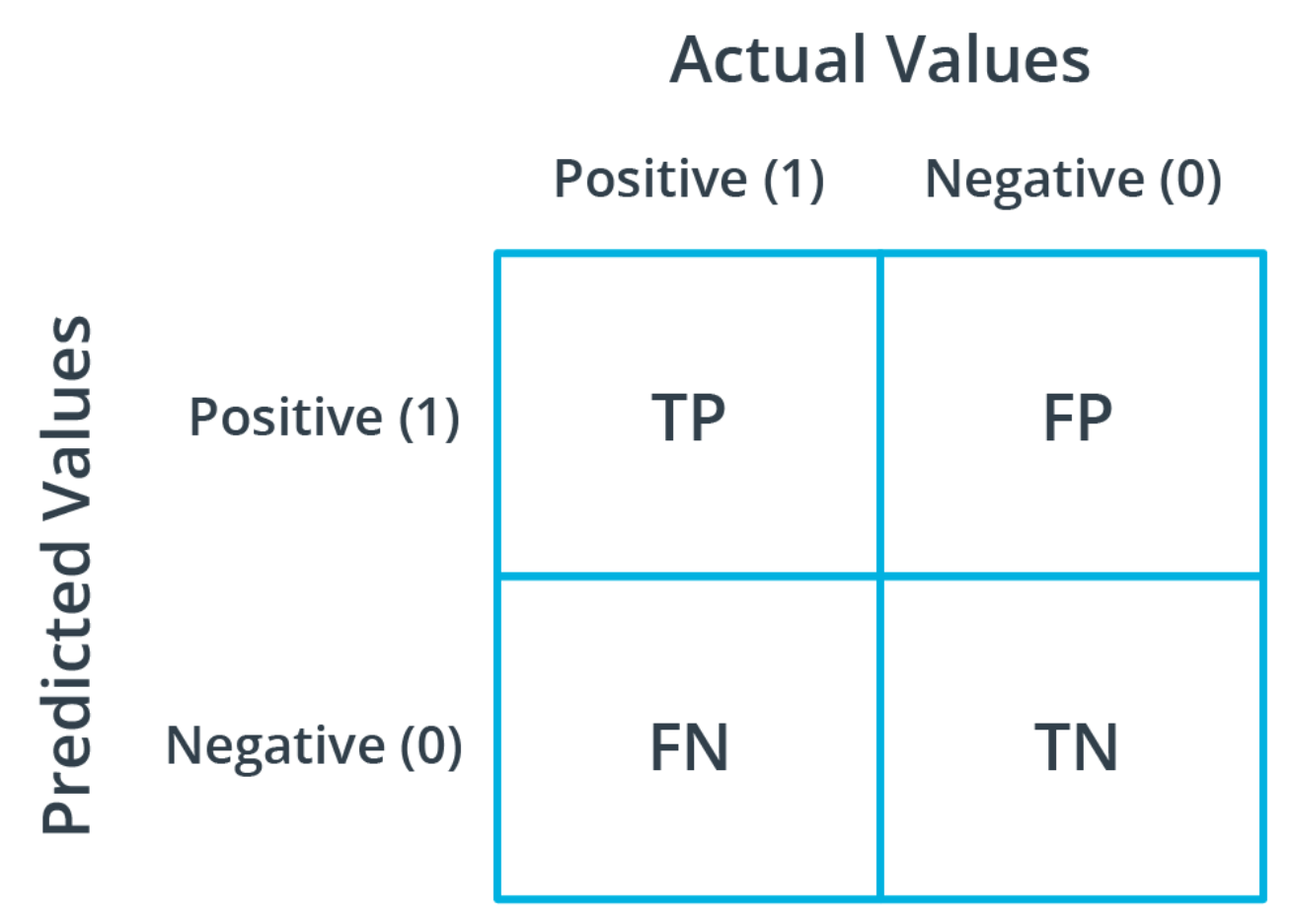
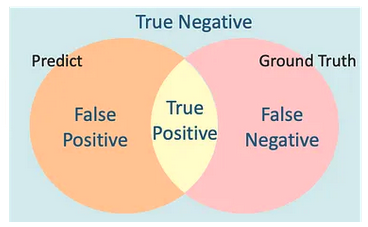
Confuion Matrix (混淆矩陣)
混淆矩陣 (Confusion Matrix) 是由 TP、FP、FN、TN 四種狀況所組合而成,可以很清楚地反映各類別之間被劃分的關係, 我們藉由此來延伸出 segmentation 的評估指標。如下:

在判斷是否為狗的模型中:
True positive (TP): 是狗且被模型判斷為狗的數量False positive (FP): 不是狗但被模型判斷為狗的數量False negative (FN): 是狗但被模型判斷為不是狗的數量True negative (TN): 不是狗且被模型判斷為不是狗的數量
在影像分割模型中:
假設圖像資料為 9 個 pixel,如下圖:

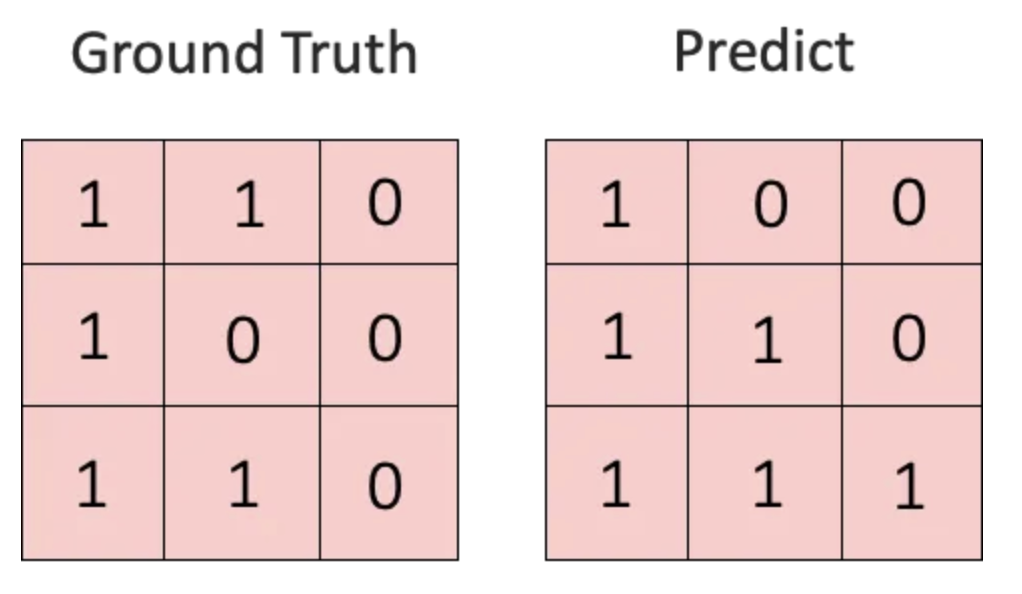
True positive (TP): 預設的 pixel 與實際皆為真的數量。False positive (FP): 預測 pixel 為真但實際為假的數量。False negative (FN): 實際 pixel 為真但預設為假的數量。True negative (TN): 預設的 pixel 與實際皆為假的數量。
此真假為 segmentation 時此 pixel 是否為我們想要的 pixel 若是則為真: 1 若不是則為假: 0
如範例:

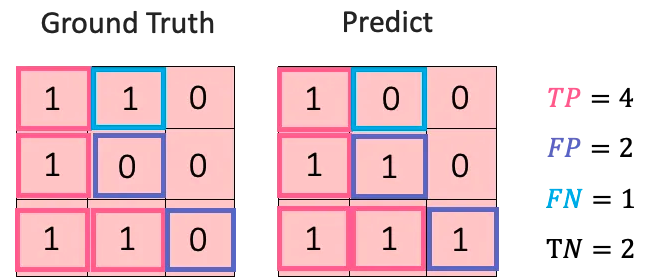
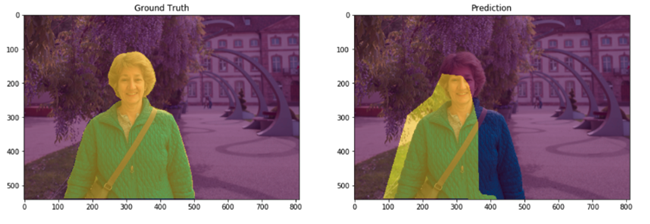
讓我們來看一下實際圖片在影像分割任務上的 TP、FP、FN、TN,如下所示:

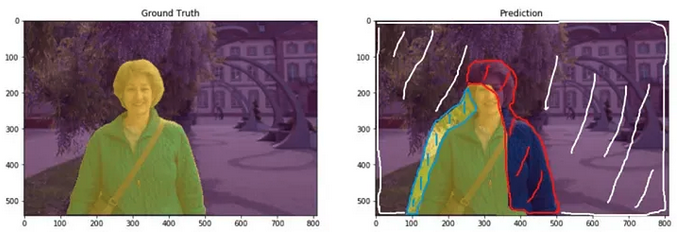
- TP: 中間黃色區塊
- FP: 左邊藍色斜線區
- FN: 右邊紅色斜線區
- TN: 白色斜線區 (背景)
Accuracy, Precision, and Recall
在影像分割中:
- Accuracy: Pixel Accuracy
- Precision: Class Pixel Accuracy
Pixel Accuracy (PA)
在所有類別預測正確的 Pixel 佔總 pixel 的比例。
PA = TP + TN / (TP + TN + FP + FN)
Class Pixel Accuracy (CPA)
在對所有預測為類別 i 的 Pixel 中 ,實際屬於類別 i 的 Pixel 的比例。
Precision = TP_{i} / (TP_{i} + FP_{i})
Example:
- Class 1: P1 = TP1 / (TP1 + FP1)
- Class 2: P2 = TP2 / (TP2 + FP2)
Mean Pixel Accuracy (MPA)
計算所有類別的 CPA 的平均值
MPA = sum(P_{i}) / 類別數量
IoU, MIoU
IoU (Intersection over Union)
IoU 是指 Ground Truth 與 Prediction 之間的交集除以聯集,由下圖的公式可以計算每個類別的 IoU。

IoU_{class} = TP / (TP + FP + FN)
Example
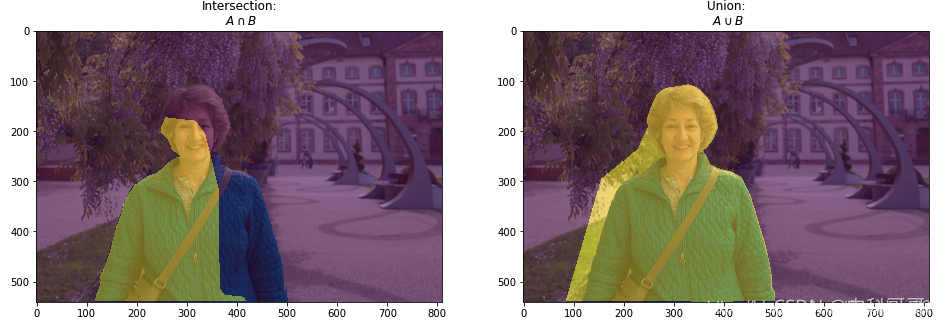
以下舉個實例:

我們分別可得到 Ground Truth 與 Prediction 之間的交集與聯集,如下:

MIoU (Mean Intersection over Union)
計算所有類別的 IoU 的平均值
MIoU = sum(IoU_{i}) / 類別數量
Dice coefficient
在分割任務中,經常使用 Dice Loss 作為 Loss function,公式如下:
$$Loss_{dice} = 1 - \frac{2|A \cap B|}{|A| + |B|}$$
其中 Dice Coefficient 為:
$$\frac{2|A \cap B|}{|A| + |B|} = \frac{2IoU}{1 + IoU}$$
Dice Coefficient 是用於計算 Ground Truth 與 Predicition 之間的相似度,|A|、|B| 分別代表 Ground Truth 和 Prediction,其值為 0~1 之間。
接下來讓我們將 Dice Coefficient 展開會發現與 F1-Score 相同:
$$ \begin{aligned} dice = \frac{2|A \cap B|}{|A| + |B|} & = \frac{2TP}{(TP+FN) + (TP+FP)} \ & = \frac{2TP}{2TP + FN + FP} = F1-score \end{aligned} $$
